A circle touches the y-axis at the point (0, 4) and cuts the x-axis in a chord of length 6 units. Then find the radius of the circle.
Circles touch the y-axis at point P(0,4).
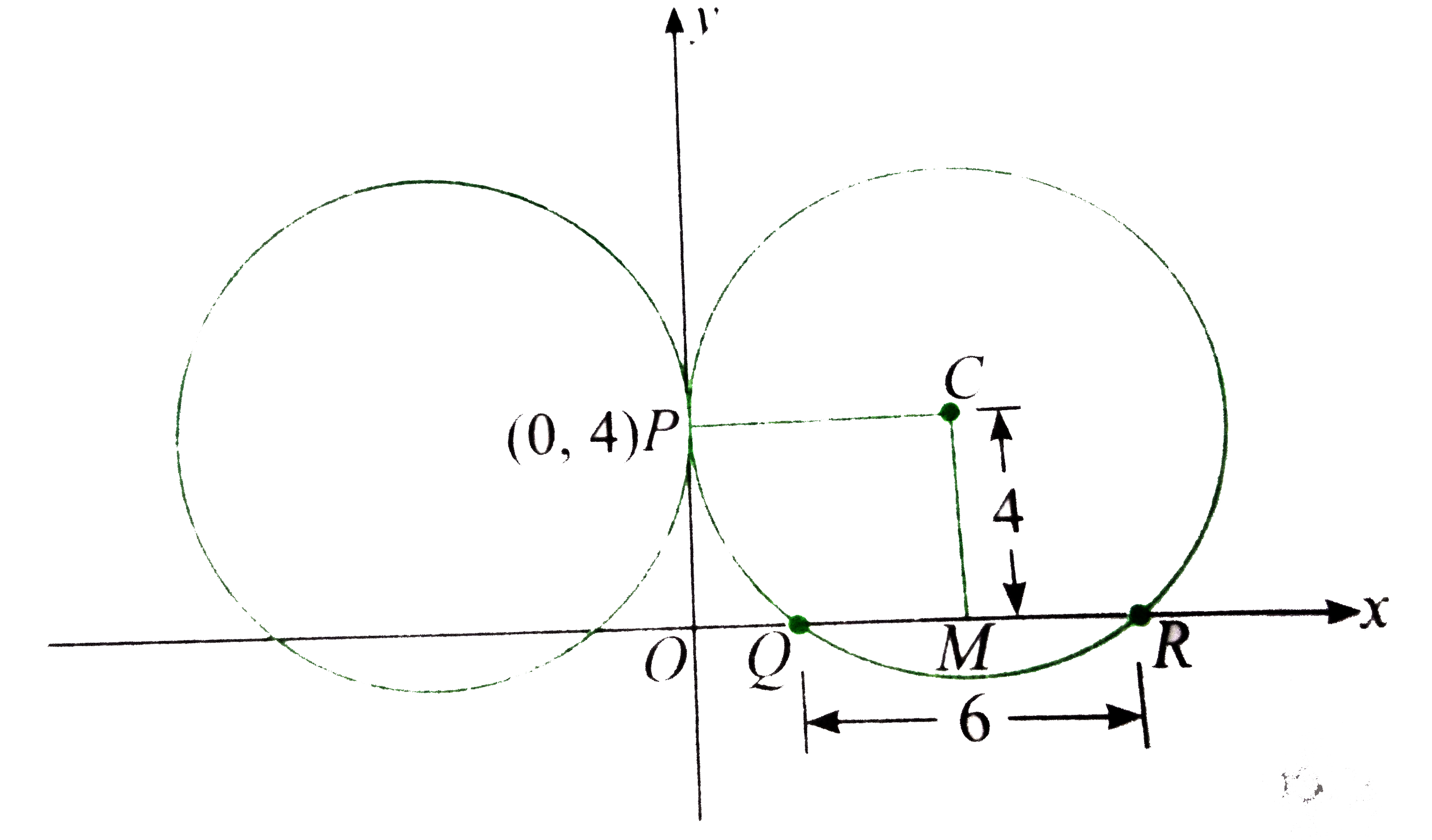
Intercept QR of circle on x-axis is 6 units
∴QM=3
Also, C is centre of one of the circles
∴CM=4
In triangle CMQ , we have
CQ2=QM2+CM2=32+42
∴CQ=5=CP= radius
Therefore, centre of the circle lying in first quadrant is C(5,4). Thus, equation of circle is (x−5)2+(y−4)2=25.
Equation of circle having centre C(-5,4) in secong quadrant is (x+5)2+(y−4)2=25.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Consider a circle C which touches the y-axis at (0,6) and cuts off an intercept 6√5 on the x - axis. Then the radius of the circle C is equal to
A√53B9C8D√82
A circle touches the y-axis at the point (0, 4) and passes through the point ( 2, 0). Which of the following lines is not a tangent to the circle ?
View SolutionThe radius of the circle touches the line y=x and has centre on the x-axis and cuts a chord of length 2 units along the line √3y−x=0 is :
View SolutionA circle with centre at (2, 4) is such that the line x+y+2=0 cuts a chord of length 6. The radius of the circle is
View SolutionA circle C is tangent to the x and y axis in the first quadrant at the points P and Q respectively. BC and AD are parallel tangents to the circle with slope –1. If the points A and B are on the y-axis while C and D are on the x-axis and the area of the figure ABCD is 900 . √2 sq. units then find the radius of the circle.
View SolutionFind the equation of the circle which touches the axis of y at a distance 4 from the origin and cuts off an intercept of length 6 on the axis of x.
View SolutionFind the radius of the circle which touches the axis of x at a distance 3 from the origin and cuts an intercept of length 6 on the axis of y.
View SolutionEquation when the circle touches the y axis at (0;β) and cuts off intercept on the x axis of length 2k.
View Solution

