Question

Find the equation of the circle having center at (2,3) and which
touches $x+y=1$

Explanation

The centre of the circle is `C (2,3)`.

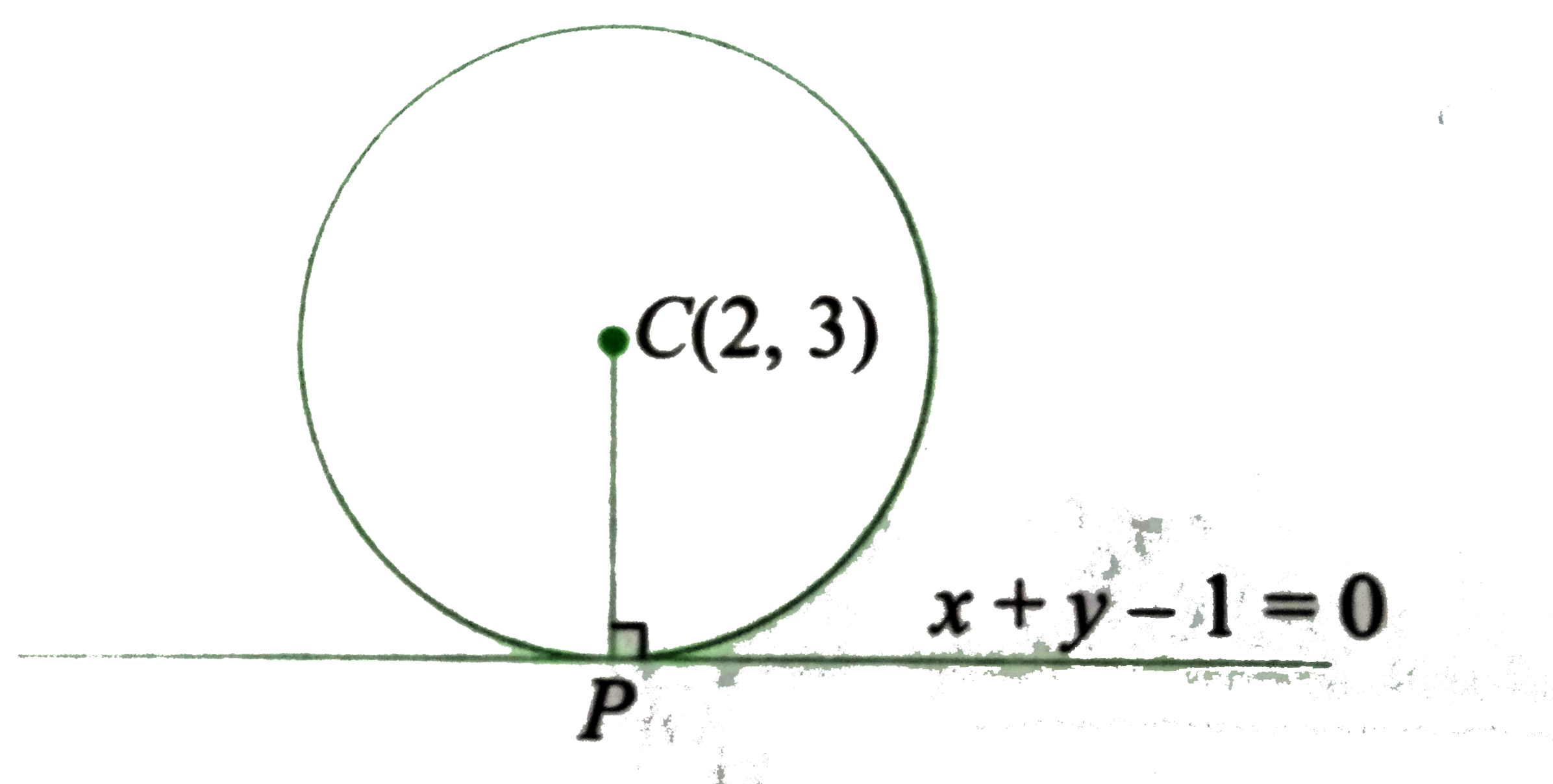
Also, line `x+y-1=0` is tangent to the circle.
Hence, the radius of the circle is the perpendicular distance of centre from the tangent.
Therefore, radius `r=CP=(|2+3-1|)/(sqrt(1^(2)+1^(2)))=2sqrt(2)`
Hence, the equation of circle is `(x-2)^(2)+(y-3)^(2)=8`