A uniform solid sphere of radius R produces a gravitational acceleration of ag on its surface. At what distance from the sphere's center are there points (a) inside and (b) outside the sphere where the gravitational acceleration is ag/2?
To solve the problem, we need to find the points where the gravitational acceleration is half of the gravitational acceleration at the surface of a uniform solid sphere. Let's denote the gravitational acceleration at the surface of the sphere as ag.
Step 1: Gravitational acceleration at the surface
The gravitational acceleration at the surface of a uniform solid sphere is given by:
ag=GMR2
where G is the gravitational constant, M is the mass of the sphere, and R is the radius of the sphere.
Step 2: Finding the point inside the sphere
For a point inside the sphere at a distance r from the center, the gravitational acceleration g is given by:
g=GM′r2
where M′ is the mass of the sphere that is at a distance r from the center. The mass M′ can be expressed as:
M′=ρ⋅43πr3
where ρ is the density of the sphere. Since the density is uniform, we can relate it to the total mass M and the total volume 43πR3:
ρ=M43πR3
Substituting M′ into the equation for g:
g=G(M43πR3)⋅43πr3r2=GMrR3
We want to find r such that:
GMrR3=ag2
Substituting ag=GMR2:
GMrR3=12⋅GMR2
Cancelling GM from both sides:
rR3=12R2
Thus:
r=R2
Step 3: Finding the point outside the sphere
For a point outside the sphere at a distance r′ from the center, the gravitational acceleration is given by:
g=GM(r′)2
We want to find r′ such that:
GM(r′)2=ag2
Substituting ag=GMR2:
GM(r′)2=12⋅GMR2
Cancelling GM from both sides:
1(r′)2=12R2
Thus:
(r′)2=2R2
Taking the square root:
r′=R√2
Final Answers
(a) The distance from the center of the sphere where the gravitational acceleration is ag2 inside the sphere is:
r=R2
(b) The distance from the center of the sphere where the gravitational acceleration is ag2 outside the sphere is:
r′=R√2
The gravitational acceleration at the surface of a uniform solid sphere is given by:
ag=GMR2
where G is the gravitational constant, M is the mass of the sphere, and R is the radius of the sphere.
For a point inside the sphere at a distance r from the center, the gravitational acceleration g is given by:
g=GM′r2
where M′ is the mass of the sphere that is at a distance r from the center. The mass M′ can be expressed as:
M′=ρ⋅43πr3
where ρ is the density of the sphere. Since the density is uniform, we can relate it to the total mass M and the total volume 43πR3:
ρ=M43πR3
Substituting M′ into the equation for g:
g=G(M43πR3)⋅43πr3r2=GMrR3
GMrR3=ag2
Substituting ag=GMR2:
GMrR3=12⋅GMR2
Cancelling GM from both sides:
rR3=12R2
Thus:
r=R2
For a point outside the sphere at a distance r′ from the center, the gravitational acceleration is given by:
g=GM(r′)2
We want to find r′ such that:
GM(r′)2=ag2
Substituting ag=GMR2:
GM(r′)2=12⋅GMR2
Cancelling GM from both sides:
1(r′)2=12R2
Thus:
(r′)2=2R2
Taking the square root:
r′=R√2
(a) The distance from the center of the sphere where the gravitational acceleration is ag2 inside the sphere is:
r=R2
r′=R√2
Topper's Solved these Questions
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
16 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
7 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - CHECKPOINT
5 Videos
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Practice questions(Integers)
4 Videos
- HEAT-MEASUREMENT AND TRANSFERBOOK - RESNICK AND HALLIDAYCHAPTER - HEAT-MEASUREMENT AND TRANSFEREXERCISE - PRACTICE QUESTIONS( INTEGER TYPE)
5 Videos
Similar Questions
A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at a distance 3R from the center of the sphere. The 1 sphere with the cavity now applies a gravitational force F2, on the same particle. Then ratio F1F2 is
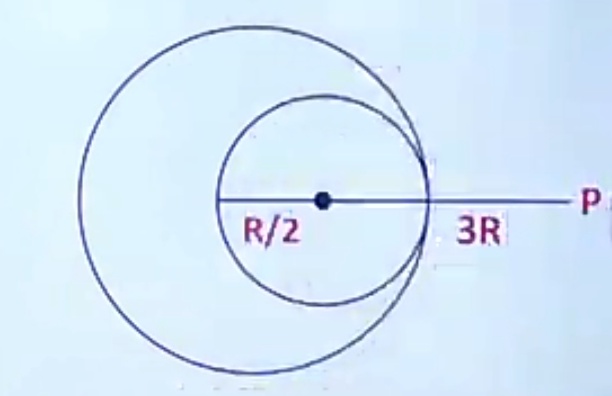
View SolutionA uniform solid of valume mass density ρ and radius R is shown in figure.
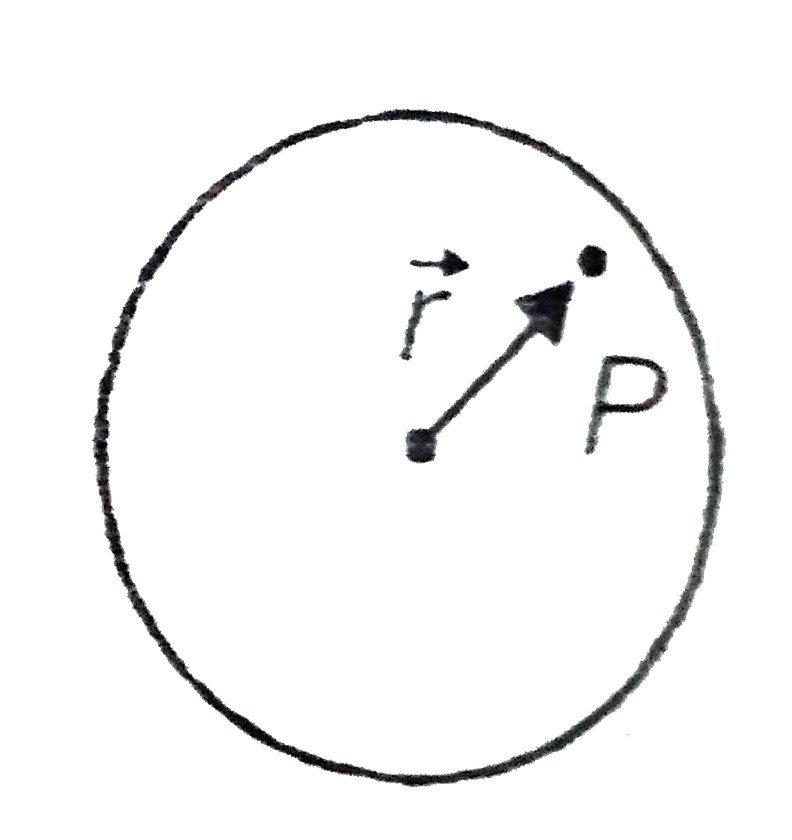
(a) Find the gravitational field at a point P inside the sphere at a distance r from the centre of the sphere. Represent the gravitational field vector →l in terms of radius vector →r of point P.
(b) Now a spherical cavity is made inside the solid sphere in such a way that the point P comes inside the cavity. The centre is at a distance a from the centre of solid sphere and point P is a distance of b from the centre of the cavity. Find the gravitational field →E at point P in vector formulationand interpret the result.
View Solution
Knowledge Check
A uniform solid sphere of radius R produces a gravitational acceleration ag on its surface. At what two distances from the centre of the sphere the acceleration due to gravity is ag/4 ?
A4R, 0.50RB2R, 0.25RC3R, 0.33RD2R, 0.50RA non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
AIncreases as r increases inside the sphereBDecreases as r increases inside as well as outsideCIncreases as increases outside the sphereDIs discontinuousat r=RIn the above question, if the soild sphere is a large rock, what is the gravitational acceleration at a point on the surface of the rock at a point just above the cavity ?
AGMR2BGM2R2CGM8R2D7GM8R2
If r the distance from the centre of the earth, then what is the nature of the graph of gravitational acceleration versus r for point below the earth's surface?
View SolutionA non-conducting solid sphere of radius R is uniformly charged. The magnitude of the electric filed due to the sphere at a distance r from its centre
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionThe gravitational field due to an uniform solid sphere of mass M and radius a at the centre of the sphere is
View SolutionA solid sphere rolling on a rough horizontal surface. Acceleration of contact point is zero.
A solid sphere can roll on the smooth surface.
View Solution
