Particle A is fixed in place at x = -0.20 m on the x axis and particle B, with a mass of 1.5 kg, is fixed in place at the origin. Particle C (not shown) can be moved along the x axis, between particle B and x=∞. shows the x component Fnet,x of the net gravitational force on particle B due to particles A and C, as a function of position x of particle C. The plot actually extends to the right, approaching an asymptote of −4.17×10−10 N as x→∞. What are the masses of (a) particle A and (b) particle C?
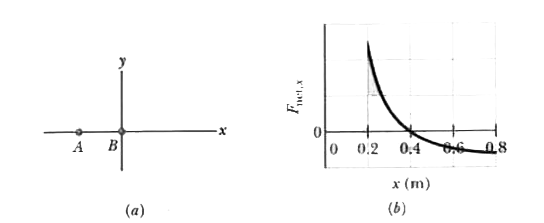
(a) 0.17kg, (b) 0.67kg
Topper's Solved these Questions
- GRAVITATIONBook:RESNICK AND HALLIDAYChapter:GRAVITATIONExercise:PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
Explore 16 Videos
- GRAVITATIONBook:RESNICK AND HALLIDAYChapter:GRAVITATIONExercise:PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
Explore 7 Videos
- GRAVITATIONBook:RESNICK AND HALLIDAYChapter:GRAVITATIONExercise:CHECKPOINT
Explore 5 Videos
- GEOMETRICAL OPTICS : REFRACTIONBook:RESNICK AND HALLIDAYChapter:GEOMETRICAL OPTICS : REFRACTIONExercise:Practice questions(Integers)
Explore 4 Videos
- HEAT-MEASUREMENT AND TRANSFERBook:RESNICK AND HALLIDAYChapter:HEAT-MEASUREMENT AND TRANSFERExercise:PRACTICE QUESTIONS( INTEGER TYPE)
Explore 5 Videos
Similar Questions
Three particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.
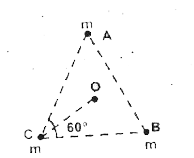
Force acting on particle C, due to particle A and B
View SolutionThree particles, each of mass m are fixed at the vertices of an equilateral triangle of side length a. The only forces acting on the particles are their mutual gravitational forces. Then answer the following questions.

Force acting on particle C, due to particle A and B
View Solution
Knowledge Check
Velocity time graphs of particles A and B moving along x-axis are shown here. Both A and B start from origin:
 AMaximum separation between the particles is 8mBMaximum separation between the particles is 10mCMaximum separation between the particles occurs at t=6sDMaximum separation between the particles occurs at t=8s
AMaximum separation between the particles is 8mBMaximum separation between the particles is 10mCMaximum separation between the particles occurs at t=6sDMaximum separation between the particles occurs at t=8sA particle is moving along the x-axis whose acceleration is given by a=3x−4, where x is the location of the particle. At t = 0, the particle is at rest at x=4/3m. The distance travelled by the particles in 5 s is
AzeroB42 mCInfiniteDNone of these
Velocity time graphs of particles A and B moving along x-axis are shown here. Both A and B start from origin:

View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionA particle of mass m is kept on the axis of a fixed circular ring of mass M and radius R at a distance x from the centre of the ring. Find the maximum gravitational force between the ring and the particle.
View SolutionFigure (a) shows an arrangement of three charged particles separted by distance d. Particles A and C are fixed on the x-axis, but particle B can be moved along a circle centered on particle A. During the movement, a radial line between A and B makes an angle θ relative to the positive direction of the x-axis (Fig. b). The curves in Fig. c give, for two situations, the magnitude Fnet of the net electrostatic force on particle A due to the other particles. That net force if given as a function of angle θ and as a multiple of a basic amount F0. For example on curve 1, at θ=180∘ we see that Fnet=2F0. (a) For the situation corresponding to curve 1, what is the ratio of the charge of particle C to that of particle B (including sign)? (b) For the situation corresponding to curve 2, what is that ratio?
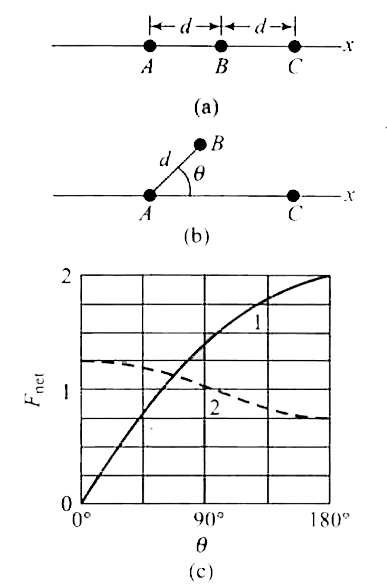
View SolutionFigure (a) shows an arrangement of three charged particles separted by distance d. Particles A and C are fixed on the x-axis, but particle B can be moved along a circle centered on particle A. During the movement, a radial line between A and B makes an angle θ relative to the positive direction of the x-axis (Fig. b). The curves in Fig. c give, for two situations, the magnitude Fnet of the net electrostatic force on particle A due to the other particles. That net force if given as a function of angle θ and as a multiple of a basic amount F0. For example on curve 1, at θ=180∘ we see that Fnet=2F0. (a) For the situation corresponding to curve 1, what is the ratio of the charge of particle C to that of particle B (including sign)? (b) For the situation corresponding to curve 2, what is that ratio?

View SolutionA particle is moving along the x-axis whose acceleration is given by a=3x−4, where x is the location of the particle. At t = 0, the particle is at rest at x=4/3m. The distance travelled by the particles in 5 s is
View Solution

