In $Δ A B C,$ right -angled at $B, A B = 5 c m and B C = 12 c m .$ find the values of $sin A, sec A, sin C and sec C .$

Video Solution

Text Solution

Verified by Experts

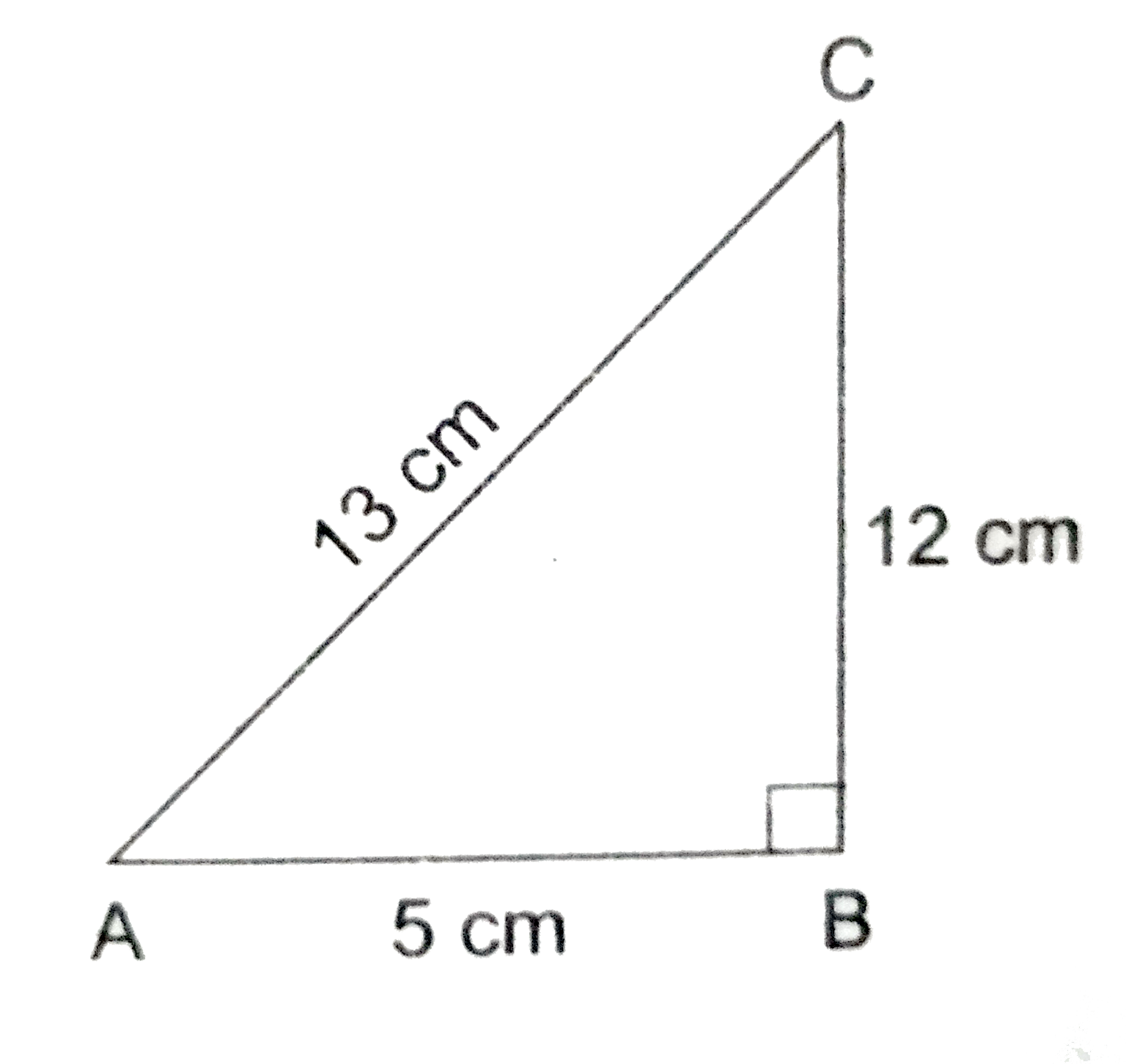
In $Δ A B C, ∠ B = 90^{\circ}, A B = 5 c m and B C = 12 c m$
By pythagoras ' theorem , we have
$A C^{2} = (A B^{2} + B C^{2}) = {{(5)}^{2} + {(12)}^{2}} c m^{2}$
$= (25 + 144) c m^{2} = 169 c m^{2} c m^{2} .$
$∴ A C = \sqrt{169 c m^{2}} = 13 c m$
For T-ratios of $∠ A,$ We have
Base $= A B = 5 c m,$
perpendicular $= B C = 12 c m$
and hypotenuse $= A C = 13 c m .$
$∴ sin A = \frac{B C}{A C} = \frac{12}{13} and sec A = \frac{A C}{A B} = \frac{13}{5} .$
for T-ratios of $∠ C,$ we have
Base $= B C = 12 c m,$
perpendicular $= A B = 5 c m$
and hypotenuse $= A C = 13 c m .$
$∴ sin C = \frac{A B}{A C} = \frac{5}{13} and sec C = \frac{A C}{B C} = \frac{13}{12} .$

Updated on:21/07/2023

$Δ A B C$ is right-angled at $C .$ If $A C = 5 c m and B C = 12 c m$ find the length of $A B .$
A17
B7
C13
D14
In $Δ A B C, ∠ B$ is right angle, AB = 5 cm and BC = 12cm , then the value of $cos C$ is :
A $\frac{5}{12}$
B $\frac{12}{5}$
C $\frac{5}{13}$
D $\frac{12}{13}$
In $Δ A B C$ , right angled at B, AB = 24 cm, BC = 7 cm. The value of $sin C$ is :
A $\frac{24}{25}$
B $\frac{7}{25}$
C $\frac{7}{24}$
DNone of these