Find the image of the point (3,8)with respect to the line x+3y=7assuming the line to be a plane mirror.
Video Solution
Text Solution
Let AB be the given line whose equation is x+3y-7=0……(i)
Now, x+3y=7⇒y=−13x+73
Slope of AB−13
Let P(3,8) be the given point and let Q(x1,y1) be its image in AB. Join PQ, intersecting AB at N. Then, PNperpendica––rPN=QN. Let the slope of PQ be m. Then, =m×(−13)=−1⇒m=3 [∴AB perpendicular PQ]
Equations of line PQ is given byy−8x−3=3⇒y−8=3x−9⇒3x−y−1=0........(ii)
On solving (i) and (ii), we get x(−3−7)=y(−21+1)=1(−1−9)⇒x−19=y−20=1−10
⇒x=1andy=2
Thus, AB and PQ intersect at the point N(1,2)
∴(3+x12=1,8+y12=2)⇒x1=−1andy1=−4
Hence the image of the given point P(3,8) is Q(-1,-4).
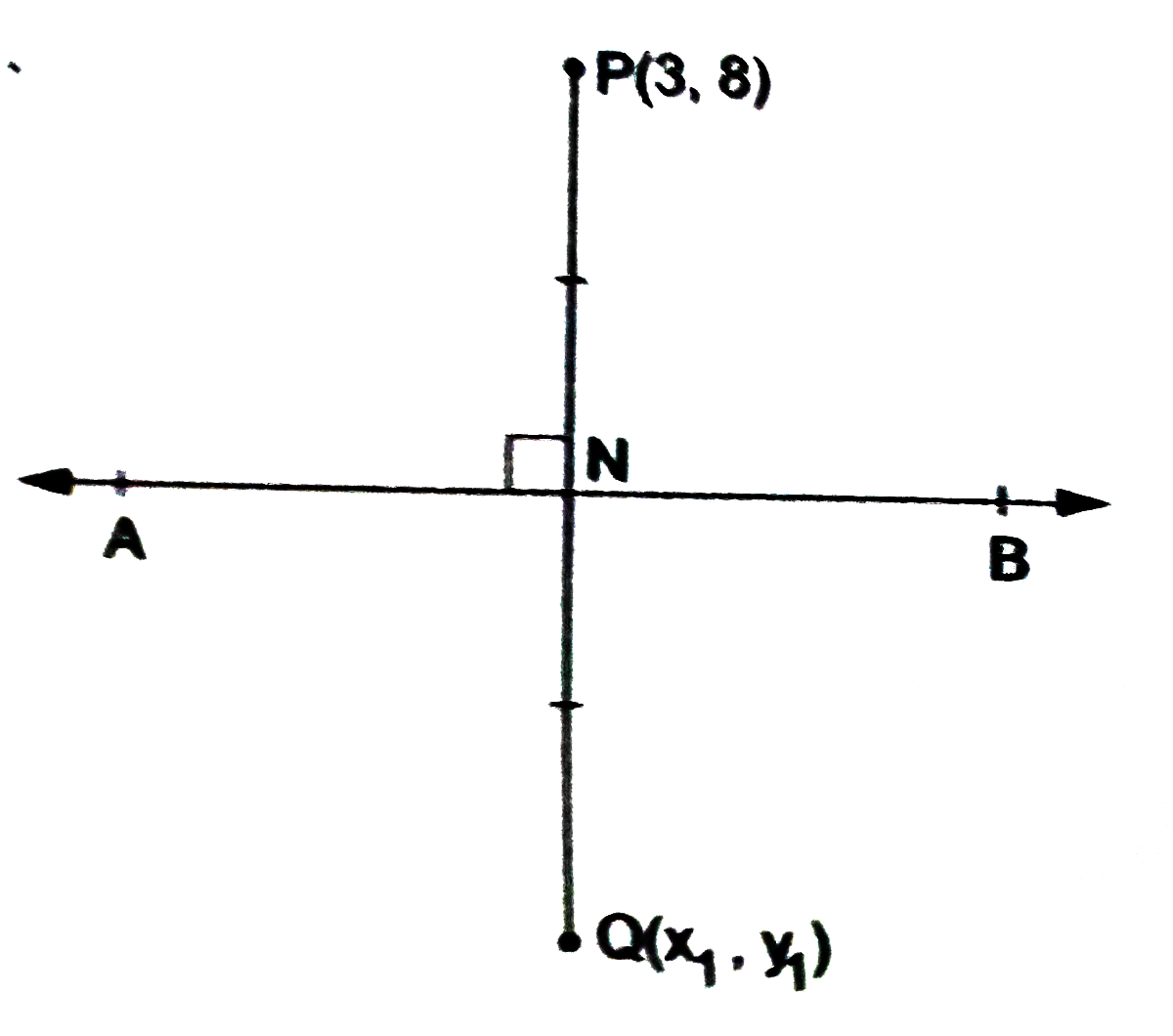
|
Topper's Solved these Questions
- STRAIGHT LINES BOOK - RS AGGARWALCHAPTER - STRAIGHT LINES EXERCISE - EXERCISE-20A
23 Videos
- STRAIGHT LINES BOOK - RS AGGARWALCHAPTER - STRAIGHT LINES EXERCISE - EXERCISE-20B
25 Videos
- STRAIGHT LINES BOOK - RS AGGARWALCHAPTER - STRAIGHT LINES EXERCISE - SOLVED-EXAMPLE
12 Videos
- STATISTICSBOOK - RS AGGARWALCHAPTER - STATISTICSEXERCISE - EXERCISE 30D
5 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - RS AGGARWALCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - EXERCISE 26 C
13 Videos
Similar Questions
Knowledge Check
Image of the point (−1,3) with respect to the line y = 2x is
A(7/5, 14/5)B(1, 2)C(3, 1)D(5, 1)The image of the point (4,-13) with respect to the line mirror 5x+y+6=0 is
A(-1,14)B(1,-14)C(-1,-14)D(1,14)The image of the point (3,8) in the line x + 3y = 7 is
A(4, 7)B(2, 3)C(- 1, - 4)DNone of these
Find the image of the point (1,−2) with respect to the line mirror 2x−y+1=0
View SolutionFind the image of the point (2,-3,4) with respect to the plane 4x+2y−4z+3=0
View SolutionFind the image of the point (−8,12) with respect to line mirror 4x+7y+13=0.
View SolutionFind the image of the point (p, q, r) with respect to the plane 2x+y+z=6. Hence find the image of the line x−12=y−21=z−34 with respect to the plane.
View SolutionFind the image of the point P(1, 2) in the line x-3y+4=0
View Solution
