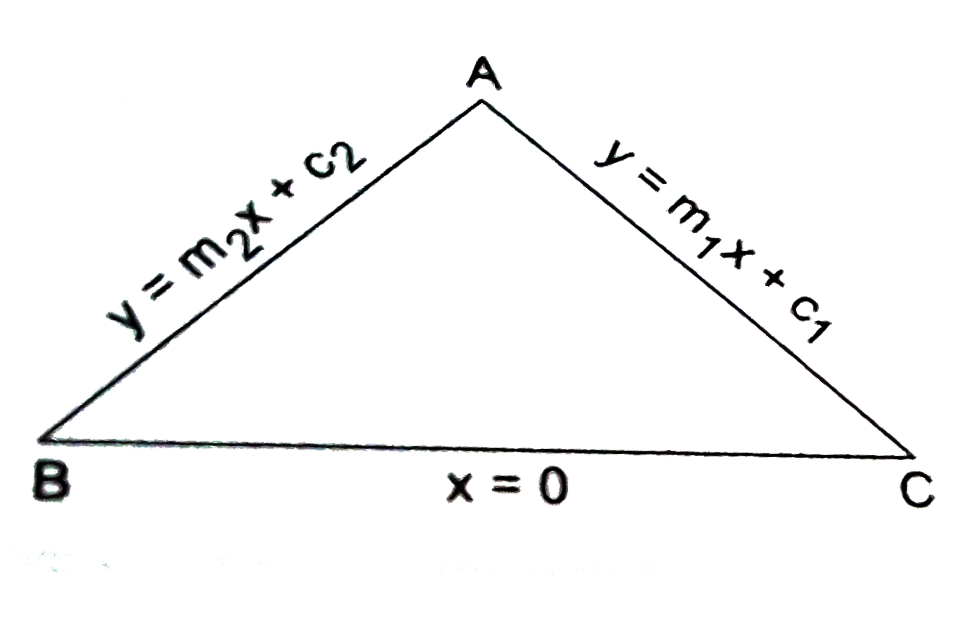
Show that the area of the triangle formed by the lines $y = m_{1} x + c_{1}, y = m_{2} x + c_{2}$ and $x = 0$ is $\frac{{(c_{1} - c_{2})}^{2}}{2 | m_{1} - m_{2} |}$

Video Solution

Text Solution

Verified by Experts

Let the sides of AC, AB and BC of $△ A B C$ be represented by all the equations:
$m_{1} x - y + c_{1} = 0 ... ... . . (i)$
$m_{2} x - y + c_{2} = 0 ... ... . . (i i)$
$x = 0 ... ... . . (i i i)$
On solving (i) and (ii) by cross multiplication, we have
$\frac{x}{(- c_{2} + c_{1})} = \frac{y}{(m_{2} c_{1} - m_{1} c_{2})} = \frac{1}{(- m_{1} + m_{2})}$
$\Rightarrow x = \frac{(c_{1} - c_{2})}{(m_{2} - m_{1})} and y = \frac{(m_{2} c_{1} - m_{1} c_{2})}{(m_{2} - m_{1})}$
Thus, the lines AC and AB intersect at A $(\frac{c_{1} - c_{2}}{m_{2} - m_{1}}, \frac{m_{2} c_{1} - m_{1} c_{2}}{m_{2} - m_{1}})$
On solving (ii) and (iii), we get $B (0, c_{2})$
On solving (i) and (iii), we get $C (0, c_{1})$
$∴ area of △ A B C is given by$
$△ = \frac{1}{2} . | x_{1} (y_{2} - y_{3}) + x_{2} (y_{3} - y_{1}) + x_{3} (y_{1} - y_{2}) |$
$= \frac{1}{2} . | \frac{(c_{1} - c_{2})}{(m_{2} - m_{1})} . (c_{2} - c_{1}) + 0 + 0 | = \frac{1}{2} . \frac{{(c_{1} - c_{2})}^{2}}{| m_{1} - m_{2} |}$
Hence the area of the triangle formed by the given line is $\frac{1}{2} . \frac{{(c_{1} - c_{2})}^{2}}{| m_{1} - m_{2} |}$

Updated on:21/07/2023

If $m_{1}, m_{2}$ be the roots of the equation $x^{2} + (\sqrt{3} + 2) x + \sqrt{3} - 1 = 0$ , then the area of the triangle formed by the lines $y = m_{1} x, y = m_{2} x$ and $y = 2$ is
A $\sqrt{33} - \sqrt{11}$ sq. units
B $\sqrt{11} + \sqrt{33}$ sq. units
C $2 \sqrt{33}$ sq. units
D121 sq. units
If $m_{1}$ and $m_{2}$ are the roots of an equation $x^{2} + (\sqrt{3} + 2) x + (\sqrt{3} - 1) = 0$ , then the area of the triangle formed by the lines $y = m_{1} x, y = m_{2} x, y = c$ is
A $(\frac{\sqrt{33} + \sqrt{11}}{4}) c^{2}$
B $(\frac{\sqrt{32} + \sqrt{11}}{16}) c$
C $(\frac{\sqrt{33} + \sqrt{10}}{4}) c^{2}$
D $(\frac{\sqrt{33} + \sqrt{21}}{4}) c^{3}$
If $m_{1}$ and $m_{2}$ are the roots of an equation $x^{2} + (\sqrt{3} + 2) x + (\sqrt{3} - 1) = 0$ , then the area of the triangle formed by the lines $y = m_{1} x, y = m_{2} x, y = c$ is
A $(\frac{\sqrt{33} + \sqrt{11}}{4}) c^{2}$
B $(\frac{\sqrt{32} + \sqrt{11}}{16}) c$
C $(\frac{\sqrt{33} + \sqrt{10}}{4}) c^{2}$
D $(\frac{\sqrt{33} + \sqrt{21}}{4}) c^{3}$