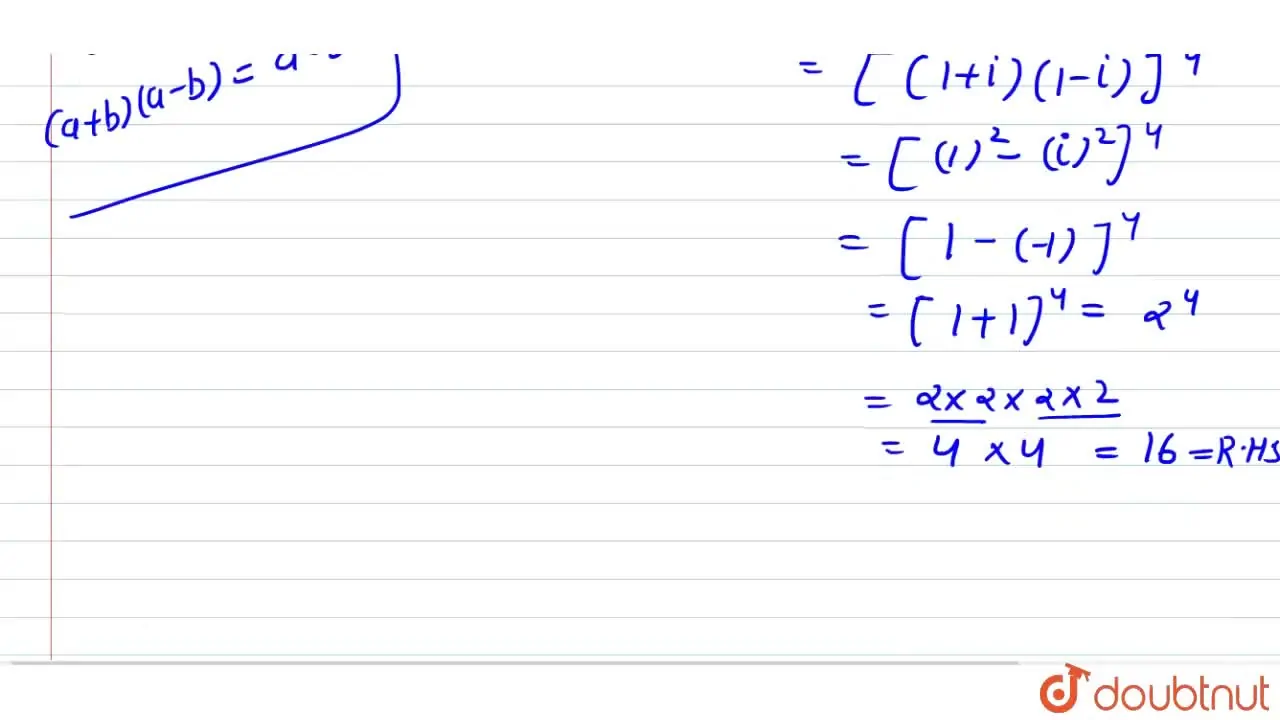FInd the value of (1+i)4×(1+1i)4
A
1
B
16
C
0
D
−1
Video Solution
Text Solution
The correct Answer is:B
We have
(i) in+in+1+in+2+in+3
=in(1+i+i2+i3)
=in(1+i−1−i)=(in×0)=0. [∵i2=−1andi3=−i]
(ii) i107+i112+i117+i122
=i107(1+i5+i10+i15)=i107(1+i4×i+i8×i2+i12×i3)
=i107(1+i+i2+i3) [∵i4=1,i8=1andi12=1]
=i107(1+i−1−i)=(i107×0)=0. [∵i2=−1,i3=−i]
(1+i)4×(1+1i)4
=(1+i)4×(1+1i×ii)4(1+i)4(1−i)4 [∵i2=−1]
={(1+i)(1−i)}4=(1−i2)4={1−(−1)}4=24=16.
|
Updated on:21/07/2023
Related Playlists
- BOOK - RS AGGARWALCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - EXERCISE 5 A15videos
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
- BOOK - RS AGGARWALCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - EXERCISE 5 B28videos
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
- BOOK - RS AGGARWALCHAPTER - COMBINATIONSEXERCISE - Exercise 9D18videos
COMBINATIONS
- BOOK - RS AGGARWALCHAPTER - CONDITIONAL IDENTITIES INVOLVING THE ANGLES OF A TRIANGLE EXERCISE - EXERCISE 1612videos
CONDITIONAL IDENTITIES INVOLVING THE ANGLES OF A TRIANGLE
Similar Questions
1) Find the value of ii
View SolutionFind the value of (1+i)6+(1−i)6
View SolutionThe value of (1+i)5×(1−i)5
View SolutionThe value of (1+i)4(1+1i)4 is
View SolutionFind the value of
i4x+1−i4x−12View SolutionFind the value of (1+i)3+(1−i)6
View SolutionThe value of (1+i)4(1−i)4 is
View SolutionThe value of (1+i)4(1−i)4 is
View SolutionFind the value of 1+i2+i4+i6
View SolutionFind the value of
(2−1×4−1)÷2−2View Solution