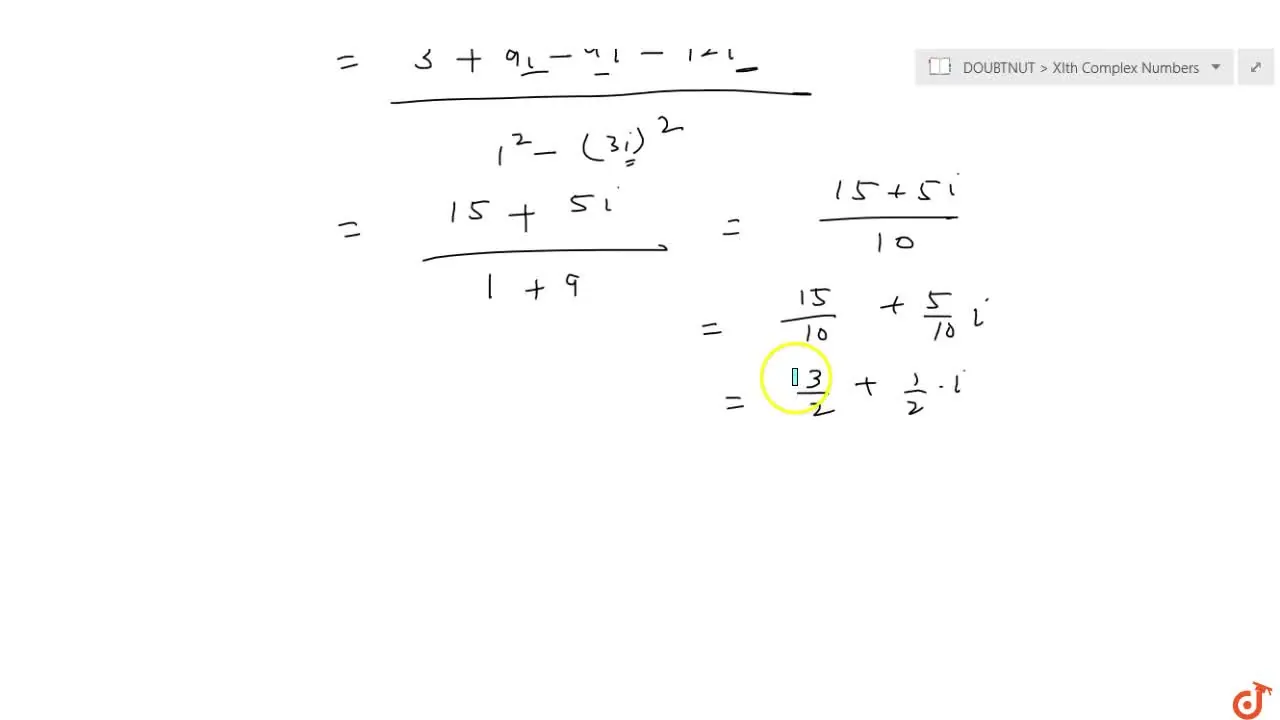Perform the indicated operation and find the result in the form a+ib:3−√−161−√−9
The correct Answer is:(32+12i)
Given expression =3−4i1−3i×1+3i1+3i=(3−4i)(1+3i)(1+9)=15+5i10=12(3+i).
Related Playlists
- BOOK - RS AGGARWALCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - EXERCISE 5 F14videos
COMPLEX NUMBERS AND QUADRATIC EQUATIONS
- BOOK - RS AGGARWALCHAPTER - COMBINATIONSEXERCISE - Exercise 9D18videos
COMBINATIONS
- BOOK - RS AGGARWALCHAPTER - CONDITIONAL IDENTITIES INVOLVING THE ANGLES OF A TRIANGLE EXERCISE - EXERCISE 1612videos
CONDITIONAL IDENTITIES INVOLVING THE ANGLES OF A TRIANGLE
Similar Questions
Perform the indicated operation and find the result in the form a+ib:3−√−161−√−9
View SolutionPerform the indicated operation and find the result in the form a+ib:2−√−251−√−16
View SolutionPerform the indicated operation and find the result in the form a+ib.
(i)2−√−251−√−16 (ii) 3−√−161−√−9View SolutionIn the following, perform the indicated operations and write the result in the form x+iy:
√3+(√3−2i)−(3−2i)View SolutionPerform the indicated operations and write the result in the form x+iy:
(i) (−3+2i)+(−6+3i)
(ii) (12+72i)−(4+52i)
(iii) (1−2i)−i+(4−7i)−2i+(5i+3).View SolutionIn the following, perform the indicated operations and write the result in the form x+iy:
i3+(6+3i)−(20+5i)+(14+3i).View SolutionIn the following, perform the indicated operations and write the result in the form x+iy:
(i) (7−2i)−(3+2i)+(7+8i)
(ii) 3−4i+2i−(8+7i)
(iii) (7−2i)−(4+i)+(−3+5i)View Solution√(1)916
View SolutionSimplify and express the result in the form (a+ib): (i)(3+√−16)−(4−√−9) (ii)(7−5i)(3+i)
View Solution3−√−161−√−25 is equal to
View Solution