If the sum of lengths of hypotenuse and a side of a right angled triangle is given, show that area of triangle is maximum, when the angle between them is π3.
Let us consider a right -angled triangle with base = x and hypotenuse = y, Let x+y=k, where k is a constant. Let θ be the angle between the base and the hypotenuse. Let A be the area of the triangle. Then,
A=12×BC×AC=12x√y2−x2
∴A2=x2(y2−x2)4=x2[(k−x)2−x2]4[∵y=(k−x)]
or A2=k2x2−2kx34...(i)
On differentiating (i), we get 2A.dAdx=2k2x−6kx24...(ii)
or dAdx=k2x−3kx24A
Now, dAdx=0⇒(k2x−3kx2)=0⇒x=k3 [neglecting x = 0]
Now, differentiating (ii), we get
2(dAdx)2+2A.d2Adx2=2k2−12kx4...(iii)
Puting dAdx=0andx=k3 in (iii), we get d2Adx2=−k24A<0
Thus, A is maximum when x=(k/3)
Now, x=k3⇒y=(k−k3)=2k3
∴xy=cosθ⇒cosθ=(k/3)(2k/3)=12⇒θ=π3
Hence, the area is maximum when θ=π3
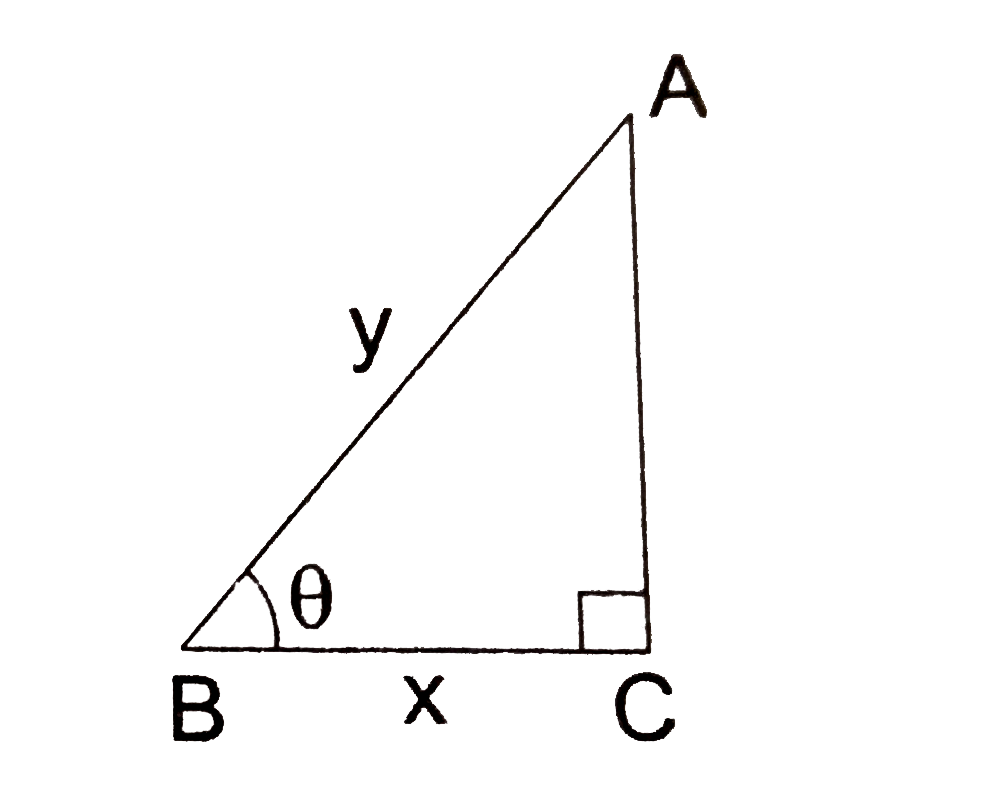
Topper's Solved these Questions
- APPLICATIONS OF DERIVATIVESBOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 11A
21 Videos
- APPLICATIONS OF DERIVATIVESBOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Exercise 11B
17 Videos
- ADJOINT AND INVERSE OF A MATRIXBOOK - RS AGGARWALCHAPTER - ADJOINT AND INVERSE OF A MATRIXEXERCISE - Exercise 7
37 Videos
- AREA OF BOUNDED REGIONS BOOK - RS AGGARWALCHAPTER - AREA OF BOUNDED REGIONS EXERCISE - Exercise 17
39 Videos
Similar Questions
If the sum of the lengths of the hypotenues and a side of a right angled triangle is given, show that the area of the triangle is maximum when the angle between them is π/3 .
View SolutionIf the sum of the lengths of the hypotenuse and another side of a right-angled triangle is given, show that the area of the triangle is maximum when the angle between these sides is π3.
View Solution
Knowledge Check
If the sum of the lengths of the hypotenuse and another side of a right-angled triangle is given, show that the area of the triangle is maximum when the angle between these sides is π3.
Aπ12Bπ4Cπ3Dπ2In the right triangle BAC,∠A=π2anda+b=8. The area of the triangle is maximum when ∠C , is
Aπ/3Bπ/4Cπ/6Dπ/2The hypotenuse of a right-angled isosceles triangle is 5 cm. The area of the triangle is (a) 5 cm2 (b) 6.25 cm2 (c) 6.5 cm2 (d) 12.5 cm2
A5 cm2B6.25 cm2C6.5 cm2D12.5 cm2
If the sum of a side and hypotenuse of a right angled triangle is given then show that area of triangle will be maximum when the angle between side and the hypotenuse is π/3.
View SolutionIf the length of the hypotenuse of a right angled triangle is 10 cm, then what is the maximum area of such a right angled triangle?
View SolutionThe maximum area of a right angled triangle with hypotenuse h is
View SolutionProve that the perimeter of a right-angled triangle of given hypotenuse is maximum when the triangle is isosceles
View SolutionFind the length of the hypotenuse of a right angled triangle if remaining sides are 9 cm and 12 cm.
View Solution
