The point of inflection of the curve y=(x−1)3 is Solution in Tamil
(0,0)
(0,1)
(1,0)
(1,1)
The correct Answer is:C
Step by step video, text & image solution for The point of inflection of the curve y=(x-1)^(3) is by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SAMPLE PAPER - 5BOOK - FULL MARKSCHAPTER - SAMPLE PAPER - 5EXERCISE - PART -II
10 Videos
- SAMPLE PAPER - 5BOOK - FULL MARKSCHAPTER - SAMPLE PAPER - 5EXERCISE - PART -III
10 Videos
- SAMPLE PAPER - 20 (UNSOLVED)BOOK - FULL MARKSCHAPTER - SAMPLE PAPER - 20 (UNSOLVED)EXERCISE - PART - IV (IV. Answer all the questions.)
14 Videos
- SAMPLE PAPER - 6 BOOK - FULL MARKSCHAPTER - SAMPLE PAPER - 6 EXERCISE - PART -IV
14 Videos
Similar Questions
If A=[8−4−5 3], verify that A(adj A)= (adj A) A= |A|I2.
View SolutionIf A=19⎡⎢⎣−8144471−84⎤⎥⎦ prove that A−1=AT.
View SolutionSolve the following system of linear equaltions, by Gaussian elimination method:
4x+3y+6z=25,x+5y+7z=13,2x+9y+z=1.
View SolutionFind the inverse of A=⎡⎢⎣211321212⎤⎥⎦ by Gauss - Jordan method.
View SolutionNumber of points of inflection of curve y=(x-2)^(6)(x-3)^(5) is
View SolutionIf the point (1,3) serves as the point of inflection of the curve y=ax^(3)+bx^(2) then the value of 'a' and 'b' are -
View SolutionConcavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)

Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
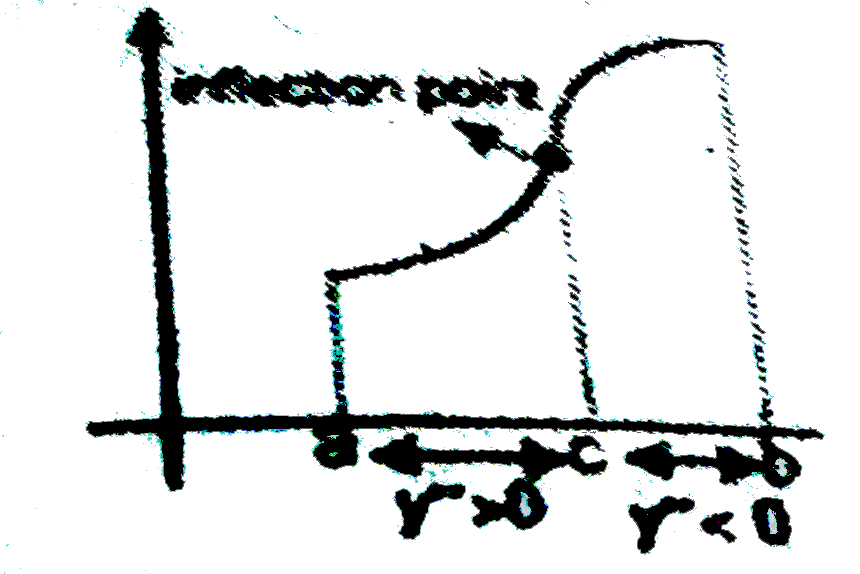
Number of point of inflection for f(x)=(x−1)3(x−2)2 is :
View SolutionConcavity Of Curve And Point Of Inflection
View SolutionFind the coordinates of the point of inflection of the curve f(x) =e^(-x^(2))
View SolutionThe point of inflection of the curve y=(x−1)3 is
View SolutionFind the inflection points of the curve y=(x−5)5/3+2 .
View SolutionDetermine the intervals of concavity of the curve f(x)=(x−2)3(x−4),x∈R and the points of inflection if any.
View SolutionThe point of inflection of the curve y=x4 is at:
View SolutionFind the points of inflection of y=x4−6x2+8x−1
View SolutionA point of inflection of the curve y=e−x2 is
View SolutionDetermine the intervals of concavity of the curve f(x)=(x−1)3(x−5),x∈R and , points of inflection if any
View Solution
