Doubtnut Promotions Sticky

Concavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)
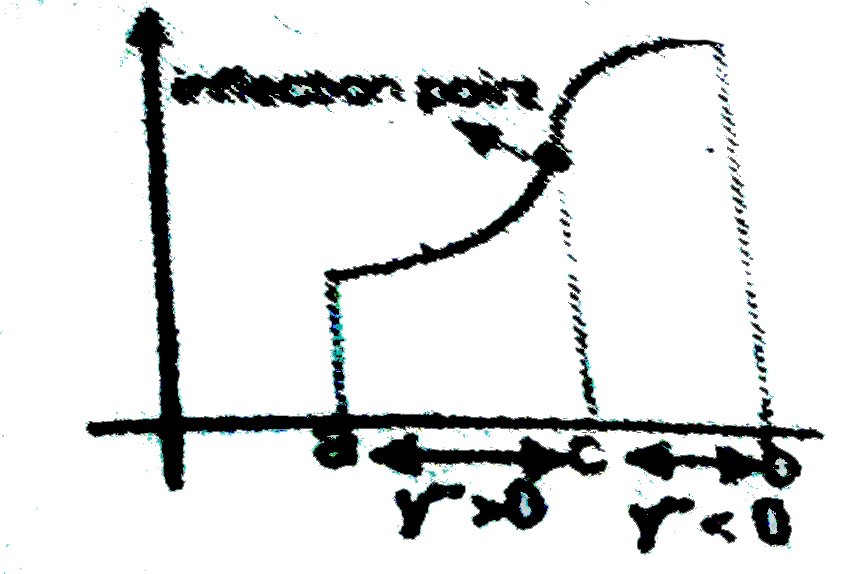
Concavity and convexity : if f''(x) gt 0 AA x in (a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and if f''(x) lt 0 AA x in (a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b) Inflection point : The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined) Number of point of inflection for f(x) =(x-1)^(3) (x-2)^(2) is :
Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
ocr_image

Number of point of inflection for f(x)=(x−1)3(x−2)2 is :

A

1

B

2

C

3

D

4

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:C

|
Answer

Step by step video, text & image solution for Concavity and convexity : if f''(x) gt 0 AA x in (a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and if f''(x) lt 0 AA x in (a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b) Inflection point : The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined) Number of point of inflection for f(x) =(x-1)^(3) (x-2)^(2) is : by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023
Class 12MATHSAPPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    Concavity and convexity :
    if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)
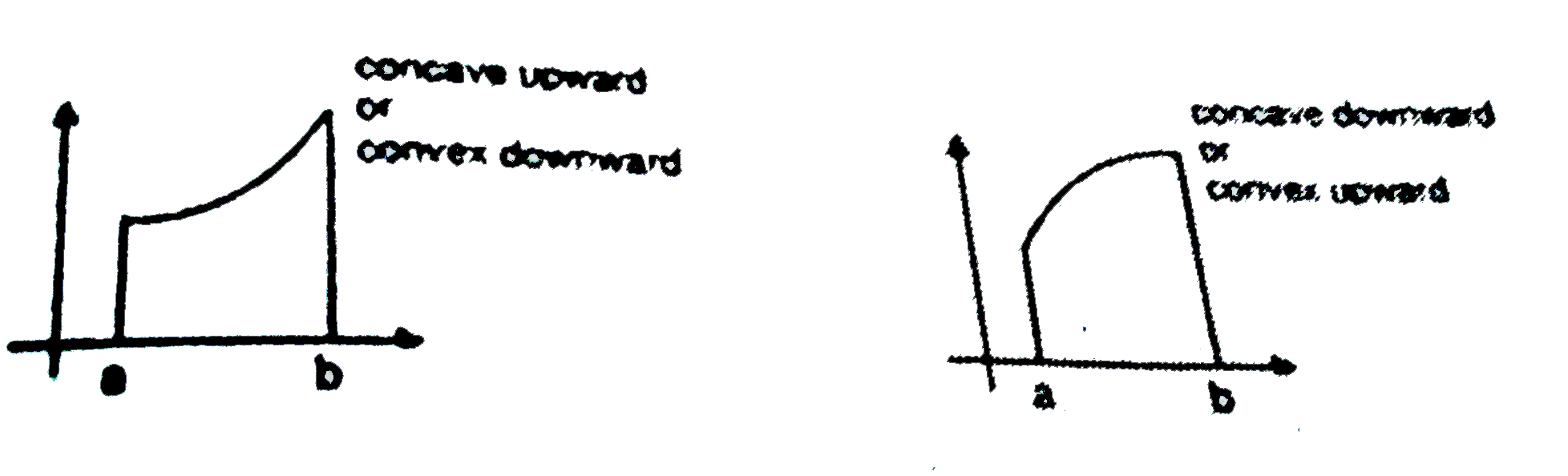
    ocr_image
    Inflection point :
    The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
    ocr_image
    Exhaustive set of values of 'a' for which the function f(x)=x4+ax3+3x22+1 will be concave upward along the entire real line is :

    A[−1,1]
    B[−2,2]
    C[0,2]
    D[0,4]
  • Question 2 - Select One

    Let g'(x)>0andf'(x)<0∀x∈R, then

    Ag(f(x+1))>g(f(x−1))
    Bf(g(x−1))<f(g(x+1))
    Cg(f(x+1))<g(f(x−1))
    Dg(g'(x+1))<g(g(x+1))
  • Question 3 - Select One

    If A and B are the points of intersection of y=f(x) and y=f−1(x), then

    AA and B necessarity lie on the line y=x
    BA and B must be coincident
    Cslope of line AB may be -1
    DNone of these above