If f''(x)<0∀x∈(a,b) and (c,f(c)) is a point lying on the curve y=f(x), where a<c<b and for that value of c, f(c) has a maximum then f'(c) equals
f(b)−f(a)b−a)
2b−a{f(b)−f(a)}
2f(b)−f(a)2b−a
0
The correct Answer is:D
To solve the problem, we need to analyze the given conditions step by step.
1. Understanding the Given Information:
We are given that f′′(x)<0 for all x in the interval (a,b). This indicates that the function f(x) is concave down on this interval.
Hint: Remember that if the second derivative is negative, the graph of the function is bending downwards.
2. Identifying the Point c:
We know that (c,f(c)) is a point on the curve where c lies in the interval (a,b) and f(c) is a maximum.
Hint: A maximum point on a curve implies that the function is not increasing at that point.
3. Applying the First Derivative Test:
Since f(c) is a maximum, we can apply the first derivative test. At a maximum point, the first derivative f′(c) must be equal to 0. This is because the slope of the tangent line at a maximum point is horizontal.
Hint: Recall that at local maxima or minima, the first derivative equals zero.
4. Conclusion:
Therefore, we conclude that:
f′(c)=0
Final Answer:
The value of f′(c) is 0.
---
We are given that f′′(x)<0 for all x in the interval (a,b). This indicates that the function f(x) is concave down on this interval.
We know that (c,f(c)) is a point on the curve where c lies in the interval (a,b) and f(c) is a maximum.
Since f(c) is a maximum, we can apply the first derivative test. At a maximum point, the first derivative f′(c) must be equal to 0. This is because the slope of the tangent line at a maximum point is horizontal.
Therefore, we conclude that:
f′(c)=0
The value of f′(c) is 0.
Topper's Solved these Questions
- Some New Pattern ProblemsBook:A DAS GUPTAChapter:Some New Pattern ProblemsExercise:Exercise
Explore 137 Videos
- Screening TestsBook:A DAS GUPTAChapter:Screening TestsExercise:Exercise
Explore 38 Videos
- Total Conditional Probability and Bayes' TheoremBook:A DAS GUPTAChapter:Total Conditional Probability and Bayes' TheoremExercise:Exercise
Explore 29 Videos
Similar Questions
Concavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)
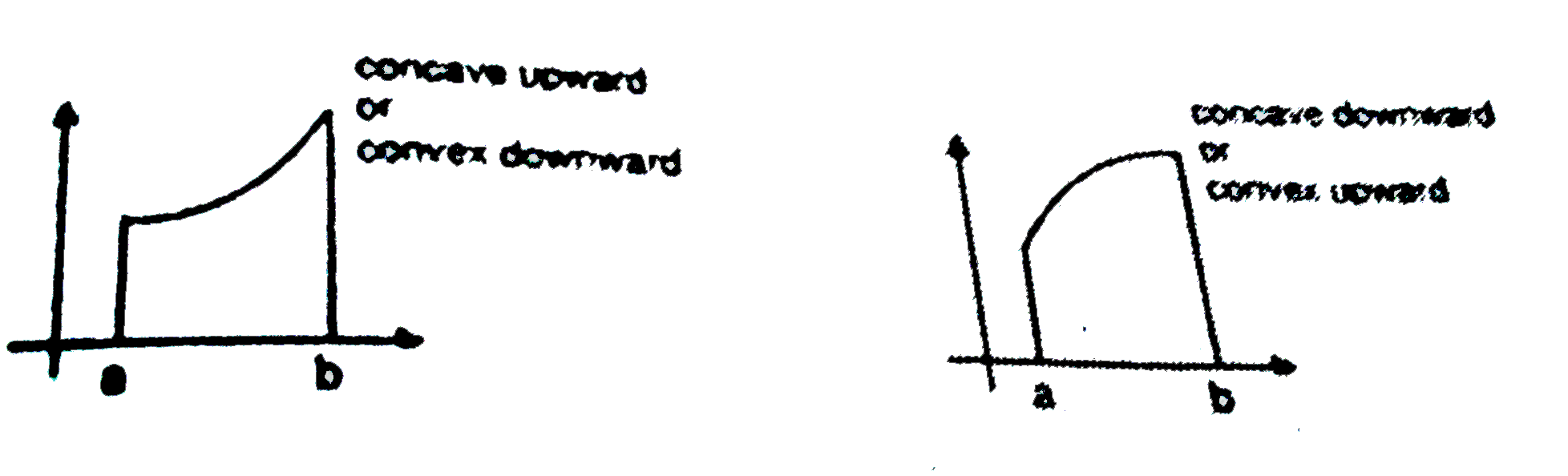
Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)

Exhaustive set of values of 'a' for which the function f(x)=x4+ax3+3x22+1 will be concave upward along the entire real line is :
View SolutionIf f''(x)<0,x∈(a,b),f(c) attains maximum value at (c,f(c)), where a < c < b, then f'(c ) is equal to :
View Solution
Knowledge Check
For every function f (x) which is twice differentiable , these will be good approximation of
∫baf(x)dx=(b−a2){f(a)+f(b)}, for more acutare results for c∈(a,b),F(c)=c−a2[f(a)−f(c)]+b−c2[f(b)−f(c)]
When c=a+b2
∫baf(x)dx=b−a4{f(a)+f(b)+2f(c)}dx
If f''(x)<0,∀x∈(a,b),and(c,f(c)) is point of maxima , where c∈(a,b), then f ' ( c) isAf(b)−f(a)b−aB3[f(b)−f(a)b−a]C2[f(b)−f(a)b−a]D0Let the definite integral be defined by the formula ∫baf(x)dx=b−a2(f(a)+f(b)). For more accurate result, for cε(a,b), we can use ∫baf(x)dx=∫caf(x)dx+∫bcf(x)dx=F(c) so that for c=a+b2 we get ∫baf(x)dx=b−a4(f(a)+f(b)+2f(c)).
If f''(x)<0∀xε(a,b) and c is a point such that a<c<b, and (c,f(c)) is the point lying on the curve for which F(c) is maximum then f'(c) is equal toAf(b)−f(a)b−aB2(f(b)−f(a))b−aC2f(b)−f(a)2b−aD0Concavity and convexity :
if f''(x)>0∀x∈(a,b) then the curve y=f(x) is concave up ( or convex down) in (a,b) and iff''(x)<0∀x∈(a,b) then the curve y=f(x) is concave down (or convex up ) in (a,b)

Inflection point :
The point where concavity of the curve changes is known as point of inflection (at inflection point f''(x) is equal to 0 or undefined)
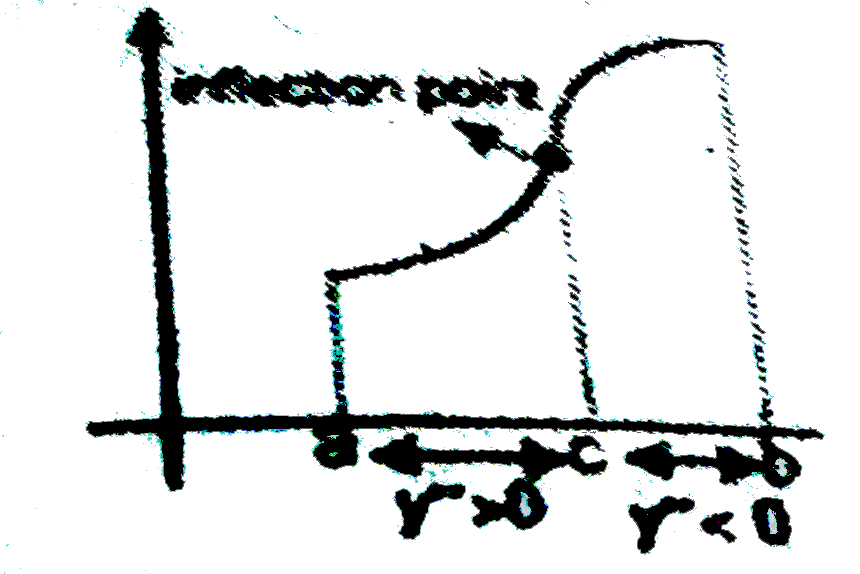
Number of point of inflection for f(x)=(x−1)3(x−2)2 is :A1B2C3D4
Let y=f(x) be a twice differentiable, non- negative function defined on [a.b]. The area ∫baf(x)dx,b> a bounded by y=f(x), the x-axis and the ordinates at x=aandx=b can be approximated as
∫baf(x)dx≈(b−a)2{f(a)+f(b)}.
Since ∫baf(x)dx=∫caf(x)dx+∫bcf(x)dx,xˆI(a,b),a better approximation to ∫baf(x)dx can be written as ∫baf(x)dx@(c−a)2{f(a)+f(c)}(b−c)2
{f(c)+f(b)}∘F(c),
If c=b−a2, then this gives:
∫baf(x)dx@b−a4{f(a)+2f(a)+2f(c)+f(b)},.......(1)
If f''(x)<0,x∈(a,b), then at the point
C(c,f(c))ony=f(x) for which F(c ) is a maximum,
f'(c) is given by
View SolutionLet f(x)<0∀x∈(≡∞,0)andf(x)>0∀x∈(0,∞) also f(0)=o, Again f'(x)<0∀x∈(−∞,−1)andf'(x)>∀x∈(−1,∞) also f'(−1)=0 given limx→∞f(x)=0andlimx→∞f(x)=∞ and function is twice differentiable.
If f'(x)<0∀x∈(0,∞)andf'(0)=1 then number of solutions of equatin f(x)=x2 is :
View SolutionLet f(x)<0∀x∈(−∞,0)andf(x)>0∀x∈(0,∞) also f(0)=0, Again f'(x)<0∀x∈(−∞,−1)andf'(x)>∀x∈(−1,∞) also f'(−1)=0 given limx→∞f(x)=0andlimx→∞f(x)=∞ and function is twice differentiable.
The minimum number of points where f'(x) is zero is:
View SolutionIf f(c) < 0 and f'(c) > 0 , then at x = c , f (x) is -
View SolutionIf f''(x)>0∀x∈R,f'(4)=0 and g(x)=f(cot2x−2cotx+5),0<x<π2 , then
View Solution

