Given P(x) =x4+ax3+bx2+cx+d such that x=0 is the only real root of P'(x) =0 . If P(-1) < P(1), then in the interval [−1,1]
P(-1) is the minimum and P(1) is the maximum of P
P(-1) is not minimum but P (1)is the maximum of P
P(-1) is the minimum and P(1) is not the maximum of P
neither P(-1) is the minimum nor P(1) is the maximum of P
The correct Answer is:B
Step by step video, text & image solution for Given P(x) =x^(4) +ax^(3) +bx^(2) +cx +d such that x=0 is the only real root of P'(x) =0 . If P(-1) < P(1), then in the interval [-1,1] by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - High Level Problems (HLP)33videos
APPLICATION OF DERIVATIVES
- BOOK - RESONANCECHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exersise-3 Part I27videos
APPLICATION OF DERIVATIVES
- BOOK - RESONANCECHAPTER - COMBINATORICSEXERCISE - Exercise-2 (Part-II: Previously Asked Question of RMO)8videos
COMBINATORICS
Similar Questions
Given P(x)=x4+ax3+cx+d such that x=0 is the only real root of P'(x)=0.IfP(1)<P(1) , then in the interval [1,1] . (1) P(1) is the minimum and P(1) is the maximum of P (2) P(1) is not minimum but P(1) is the maximum of P (3) P(1) is the minimum but P(1) is not the maximum of P (4) neither P(1) is the minimum nor P(1) is the maximum of P
View SolutionLetf(x)=x4+ax3+bx2+cx+d be a polynomial with real coefficients and real roots. If |f(i)|=1where i=√−1, then the value of a +b+c+d is
View Solution
Knowledge Check
- Question 1 - Select One
Given P(x) =x4+ax3+bx2+cx+d such that x=0 is the only real root of P'(x) =0 . If P(-1) lt P(1),then∈the∫erval[-1,1]
A(a) P(-1) is the minimum and P(1) is the maximum of PB(b) P(-1) is not minimum but P(1) is the maximum of PC(c) P(-1) is not minimum and P(1) is not the maximum of PD(d) neither P(-1) is the minimum nor P(1) is the maximum of P - Question 2 - Select One
The condition that the roots of ax3+bx2+cx+d=0 may be in G.P is
Aa3b=c3dBab3=cd3Cc3a=b3dDca3=bd3 - Question 3 - Select One
If x2+x+1 is a factor of ax3+bx2+cx+d, then the real root of ax3+bx2+cx+d=0 is
A−d/aBd/aCa/dDnone of these
If P(x)=x4+ax3+bx2+cx+d,P(1)=P2=P(3)=0 then find P(4)
View SolutionIn the given figure graph of y=p(x)=x4+ax3+bx2+cx+d is given
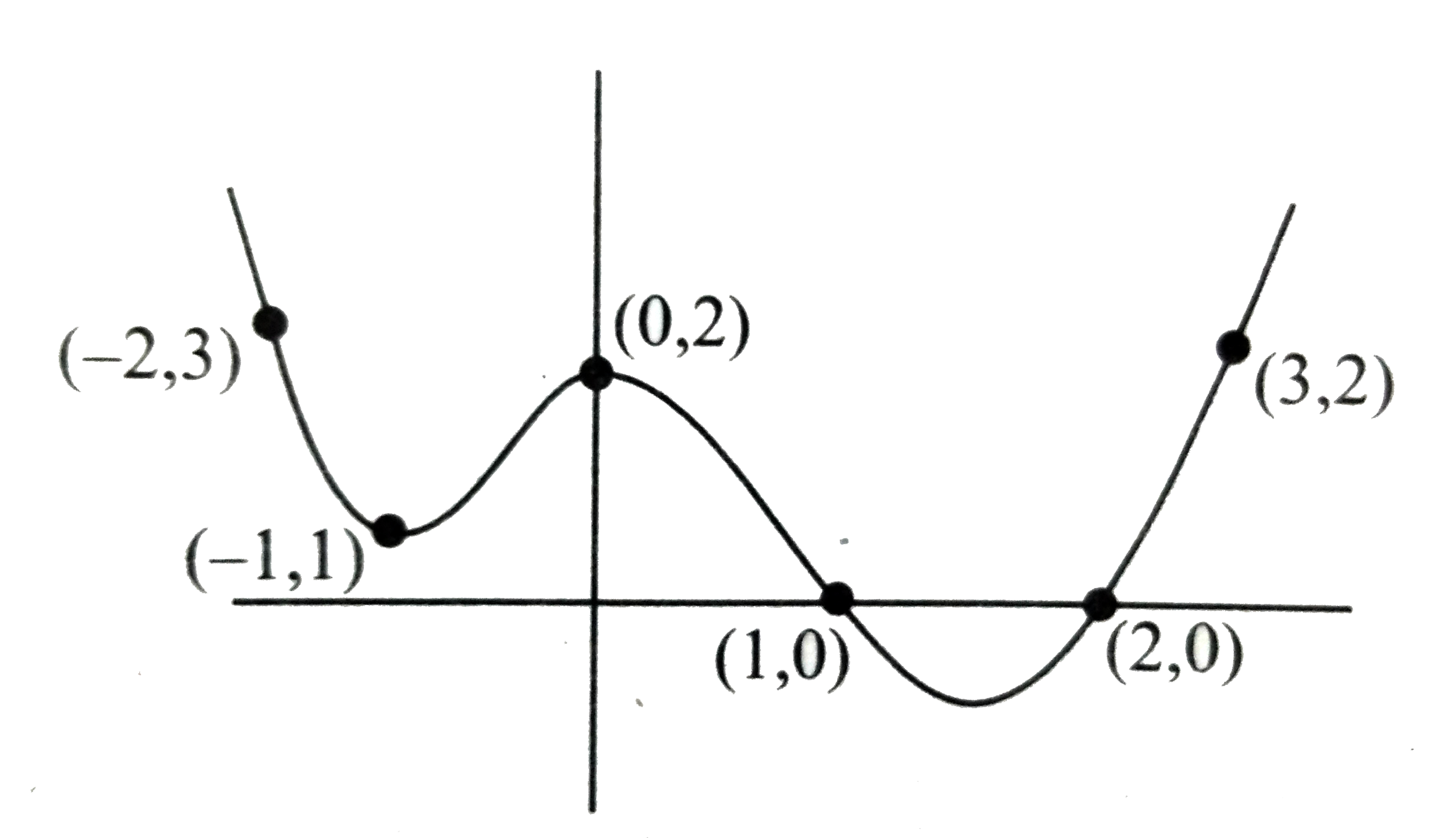
The product of all imaginery roots of p(x)=(0) isView SolutionIn the given figure graph of y=P(x)=ax5+bx4+cx3+dx2+ex+f, is given.

The minimum number of real roots of equation (P''(x))2+P'(x).P'''(x)=0, isView SolutionLet f(x)=ax3+bx2+cx+d,a≠0 If x1andx2 are the real and distinct roots of f'(x)=0 then f(x)=0 will have three real and distinct roots if
View SolutionLet P(x)=x4+ax3+bx2+cx+d, where a,b,c,d∈R.Suppose P(0)=6,P(1)=7,P(2)=8andP(3)=9, then find the value of P(4).
View Solution

