Two concentric coplanar circular loops made of wire with resistance per unit length 10−4Ω/m, have diameters 0.2 m and 2m. A time varying potential difference (4+2.5t) volt is applied to the larger loop. Calculate the current in the smaller loop.
The resistance of the loops
R1=2πr1×10=2π×0.1×10
=6.28Ω
and R2=2πr2=2π×1×10
=62.8Ω
Flux in the smaller loop ϕ=B2A1
=μ0i22r2πr21
=μ0i22r2πr21
=μ0[VR2]πr212r2
=μ0[4+2.5t]R2πr212r2
The induced curretn i1=eR1=[dϕ/dt]R1
After substituting the value and simplifying we get
i=1.25A
Topper's Solved these Questions
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBook:DISHA PUBLICATIONChapter:CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSExercise:CHAPTER -21 : (ALTERNATING CURRENT)
Explore 15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBook:DISHA PUBLICATIONChapter:CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSExercise:CHAPTER 22 : (ELECTROMAGNETIC WAVES)
Explore 15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBook:DISHA PUBLICATIONChapter:CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSExercise:CHAPTER 19 : (MAGNETISM AND MATTER)
Explore 14 Videos
- ATOMSBook:DISHA PUBLICATIONChapter:ATOMSExercise:EXERCISE-2: CONCEPT APPLICATOR
Explore 30 Videos
- COMMUNICATION SYSTEM Book:DISHA PUBLICATIONChapter:COMMUNICATION SYSTEM Exercise:EXERCISE-2 : Concept Applicator
Explore 30 Videos
Similar Questions
Two concentric coplanar circular loops made of wire, with resistance per unit length λ , have radii rI and r2(r2>>rI) . A potential difference (α+βt) is applied to the larger loop, where t is time. Calculate current in the smaller loop.
View SolutionA very small circular loop of area 5×I0−4m2 , resistance 2Ω and negligible inductance is initially coplanar and concentric with a much larger fixed circular loop of radius 0.Im . A constant current of IA is passed in the bigger loop and the smaller loop is rotated with angular velocity ωrad/sec about a diameter. Calculate (a) the flux limked with the smaller loop, (b) indced emf (c) induced current in the smaller loop, as a function of time.
View Solution
Knowledge Check
Two concentric, coplanar circular loop of wire, with different diameter carry current in the same sense as shown in the figure. Which of the following statement(s) is //are correct?
 Athe magnetic force exerted by the outer loop on a short portion of the inner loop is radially outwardBthe magnetic force exerted by the outer loop on a short portion of the inner loop is radially inwardCthe net megnetic force exerted by the outer loop on a whole inner loop is non zero and is radially outwardDthe net magnetic force exerted by the outer loop on a whole inner loop is zero
Athe magnetic force exerted by the outer loop on a short portion of the inner loop is radially outwardBthe magnetic force exerted by the outer loop on a short portion of the inner loop is radially inwardCthe net megnetic force exerted by the outer loop on a whole inner loop is non zero and is radially outwardDthe net magnetic force exerted by the outer loop on a whole inner loop is zeroA very small circular loop of radius a is initially coplanar & concentric with a much larger circular loop of radius b (>>a). A constant current is passed in the large loop which is kept fixed in space & the small loop is rotated with angular velocity omega about a diameter. The resistance of the small loop is R & its self inductance is negligible. The current in the larger loop is clockwise.
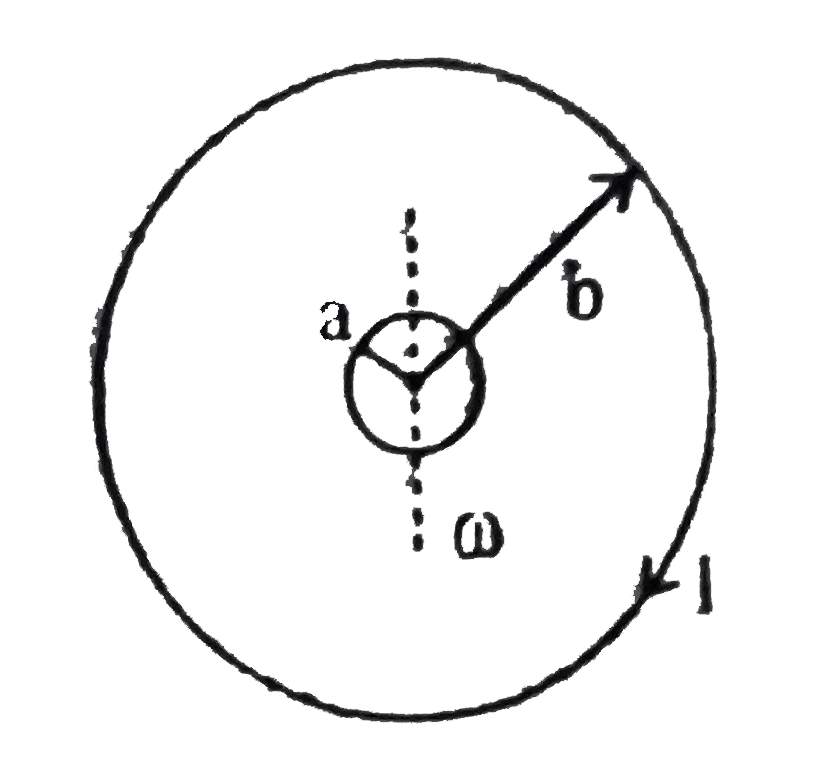
Find the current in the small loop as a function of time.Aπa2μ0Iωsinωt2bRBπa2μ0Iωcosωt2bRCπb2μ0Iωsinωt2aRDπb2μ0Iωcosωt2aRA very small circular loop of radius a is initially (at t = 0) coplanar and concentric with a much larger fixed circular loop of radius b. A constant current I flows in the larger loop. The smaller loop is rotated with a constant angular speed ω about the common diameter. The emf induced in the smaller loop as a function of time t is
Aπa2μ0I2bωcos(ωt)Bπa2μ0I2bωsin(ω2t2)Cπa2μ0I2bωsin(ωt)Dπa2μ0I2bωsin2(ωt)
A potentiometer consists of a wire of length 4 m and resistance 10Ω. If is connected of cell of emf 2V. The potential difference per unit length of the wire will be
View SolutionA large circular loop of radius 1 metre has total resistance 4Ω. A variable current is folwing through the loop. The current at any instant is given by equation l = lA, where i is time in second. A very small circular loop or radius 1 cm having resistance 3.14 Ω is placed coaxially with the larger loop at a distance of √3 metre from the centre of larger loop. If induced current in smaller loop is μ0x×10−416 ampere then, find x.
View SolutionA conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v0 , parallel to an infinite conducting wire carrying current i0. A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v02 along the direction 2 of the current. At the instant t=0, the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop.

(a) The current through the rod when it is at a distance of (a2) from the point A of the loop.
(b) Force required to maintain the velocity of the rod at that instant.
View SolutionA current i=αt , where t is time is flowing in a long wire. A smaller circular loop of radius a has its plane parallel to the wire and is placed at distance d from the wire. If resistance per unit length of loop is λ , find the magnitude and direction of the current in the loop.
View SolutionA circular brass loop of radius a and resistance R is placed with it plane perpendicular to a magnetic field, which varies with time as B=B0sinωt. Obtain the expression for the induced current in the loop.
View Solution