The current in an RL circuits drops from 1.0 A to 10 mA in the 10 second following removal of the battery from the circuti. If L is 10 H, find the resistance R (in ohm) in the circuit.
To solve the problem, we need to find the resistance R in an RL circuit where the current drops from 1.0A to 10mA in 10s after the battery is removed. The inductance L is given as 10H.
1. Convert the Current Values:
- Initial current I0=1.0A
- Final current I=10mA=10×10−3A=0.01A
2. Use the RL Circuit Current Decay Formula:
The current in an RL circuit after the battery is removed can be expressed as:
I=I0e−tτ
where τ (the time constant) is given by:
τ=LR
3. Rearranging the Formula:
We can rearrange the formula to express τ:
II0=e−tτ
Taking the natural logarithm on both sides:
−tτ=ln(II0)
Thus,
τ=−tln(II0)
4. Substituting the Known Values:
- t=10s
- I=0.01A
- I0=1.0A
Substitute these values into the equation:
τ=−10ln(0.011.0)
5. Calculating the Natural Logarithm:
ln(0.011.0)=ln(0.01)=ln(10−2)=−2ln(10)≈−2×2.303=−4.606
Therefore,
τ=−10−4.606≈2.169s
6. Relating τ to Resistance R:
We know that:
τ=LR
Rearranging gives:
R=Lτ
7. Substituting the Values:
- L=10H
- τ≈2.169s
So,
R=102.169≈4.61Ω
Final Answer:
The resistance R in the circuit is approximately 4.61Ω.
- Initial current I0=1.0A
- Final current I=10mA=10×10−3A=0.01A
The current in an RL circuit after the battery is removed can be expressed as:
I=I0e−tτ
where τ (the time constant) is given by:
τ=LR
We can rearrange the formula to express τ:
II0=e−tτ
Taking the natural logarithm on both sides:
−tτ=ln(II0)
Thus,
τ=−tln(II0)
- t=10s
- I=0.01A
- I0=1.0A
τ=−10ln(0.011.0)
ln(0.011.0)=ln(0.01)=ln(10−2)=−2ln(10)≈−2×2.303=−4.606
Therefore,
τ=−10−4.606≈2.169s
We know that:
τ=LR
Rearranging gives:
R=Lτ
- L=10H
- τ≈2.169s
R=102.169≈4.61Ω
The resistance R in the circuit is approximately 4.61Ω.
Topper's Solved these Questions
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER -21 : (ALTERNATING CURRENT)
15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 22 : (ELECTROMAGNETIC WAVES)
15 Videos
- CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSBOOK - DISHA PUBLICATIONCHAPTER - CHAPTERWISE NUMERIC /INTEGER ANSWER QUESTIONSEXERCISE - CHAPTER 19 : (MAGNETISM AND MATTER)
14 Videos
- ATOMSBOOK - DISHA PUBLICATIONCHAPTER - ATOMSEXERCISE - EXERCISE-2: CONCEPT APPLICATOR
30 Videos
- COMMUNICATION SYSTEM BOOK - DISHA PUBLICATIONCHAPTER - COMMUNICATION SYSTEM EXERCISE - EXERCISE-2 : Concept Applicator
30 Videos
Similar Questions
The current in an RL circuit drops from 2.30 A to 3.40 mA in 0.025 s following removal of the battery from the circuit. If L is 10 H, find the resistance R in the circuit.
View SolutionThe current in a discharging LR circuit without the battery drops from 2.0 A to 0.10 s. (a) find the time constant of the circuit. (b) if the inductance of the circuit is 4.0 H, what is its resistance?
View Solution
Knowledge Check
In the circuit shown, total power supplied by an ideal battery is 80 W. if R=10Ω. Then
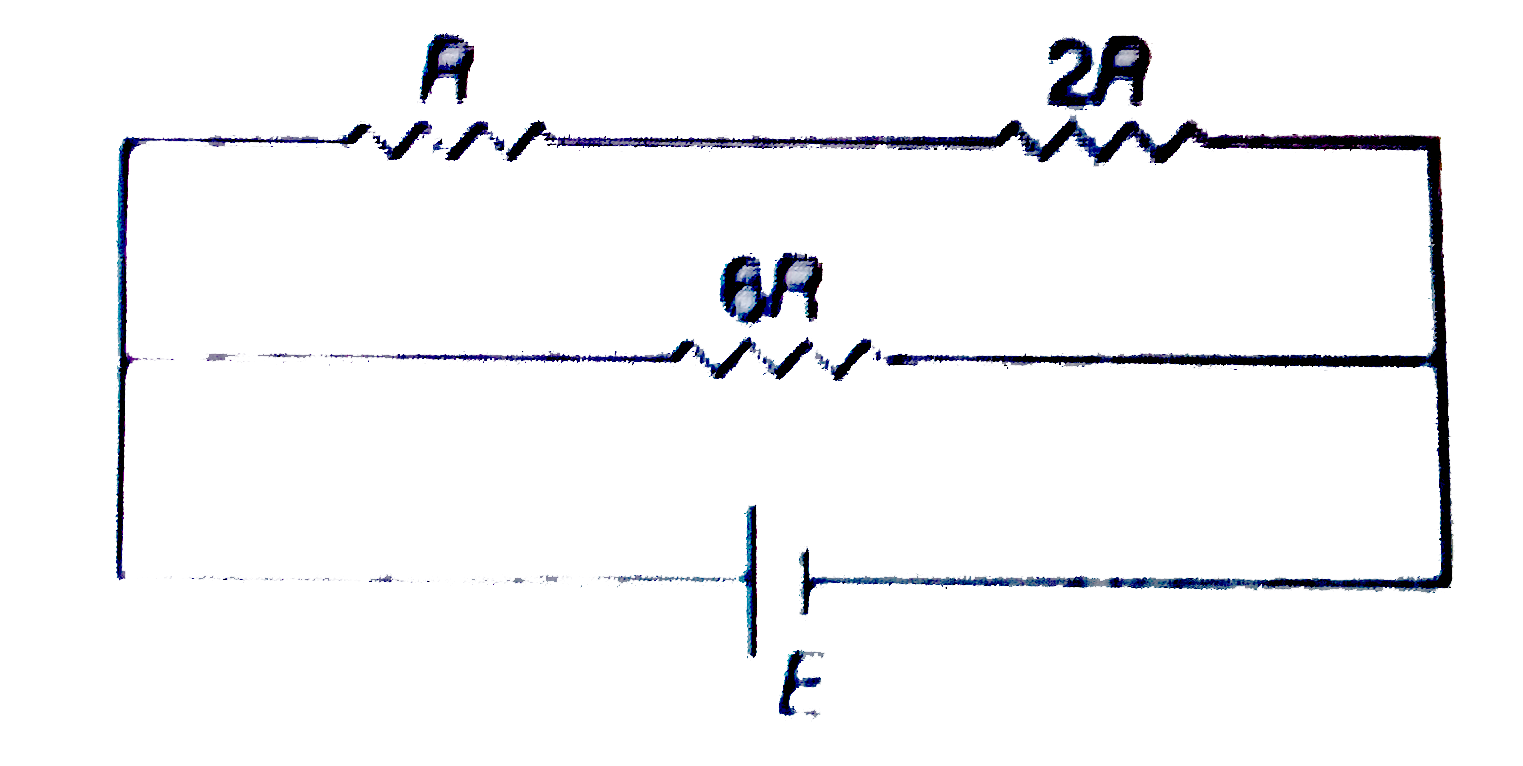
If the resistance R is removed from the circuit. ThenApower consumed by 2R will increaseBpower consumed by 6R will increaseCboth (a) and (b) are correctDboth (a) and (b) wrongIn the circuit, the current flowing through 10Ω resistance is
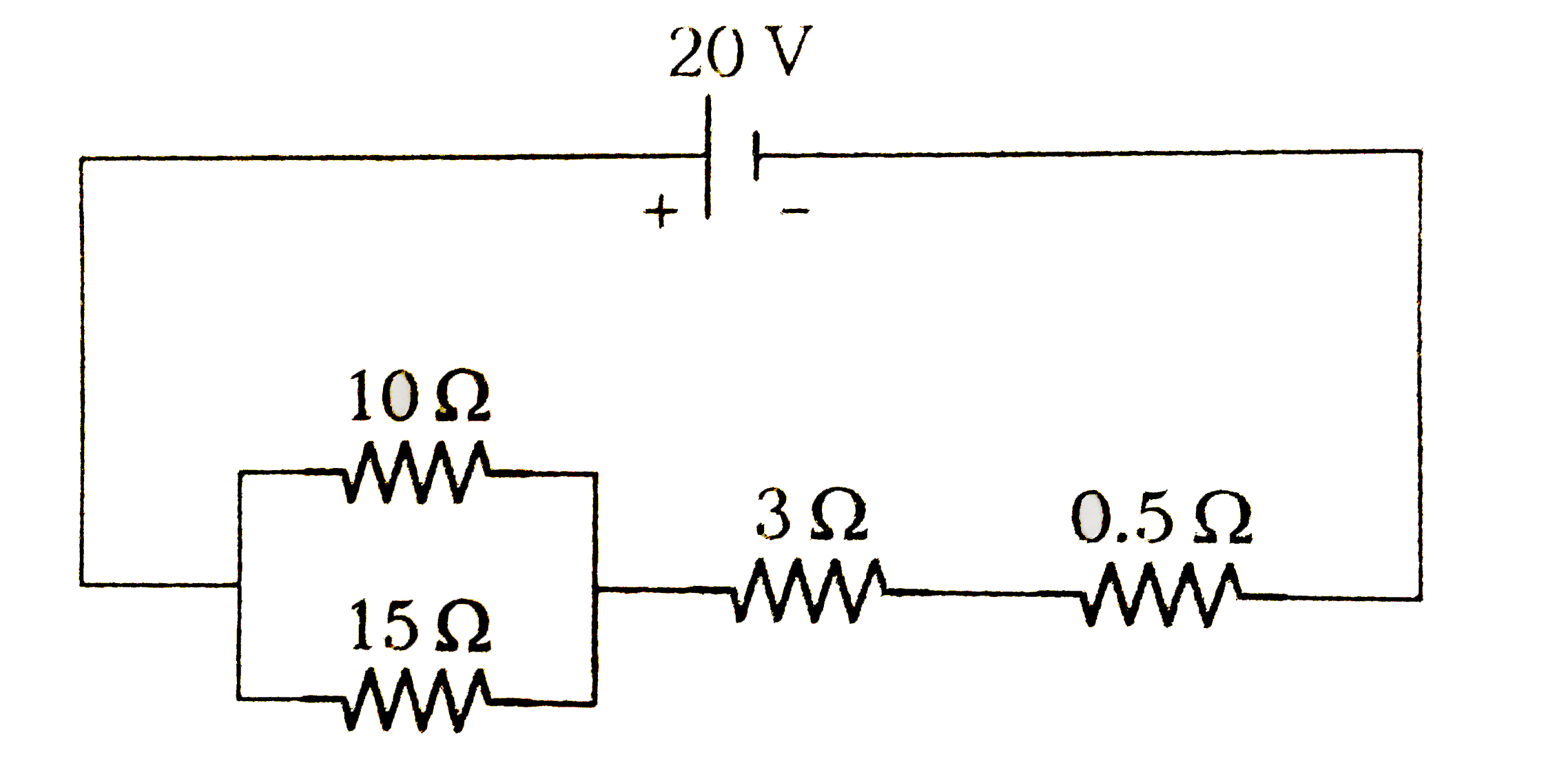 A12AB1.2AC0.8AD0.4A
A12AB1.2AC0.8AD0.4AThe current in a simple series circuit is 5.0 amp . When an additional resistance of 2.0 ohms is inserted, the current drops to 4.0 amp . The original resistance of the circuit in ohms was
A1.25B8C10D20
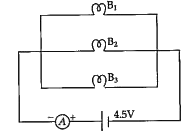
Total current flowing from the battery is 1A. Find the total resistance of the circuit:
View SolutionConsider the circuits shown in fing Both the circuits are taking same current from the battery, but the current through R in the second circuit is 1//10 th of the current thourgh R in the first cirucit , if R is 11Ω then find the value of R1andR2
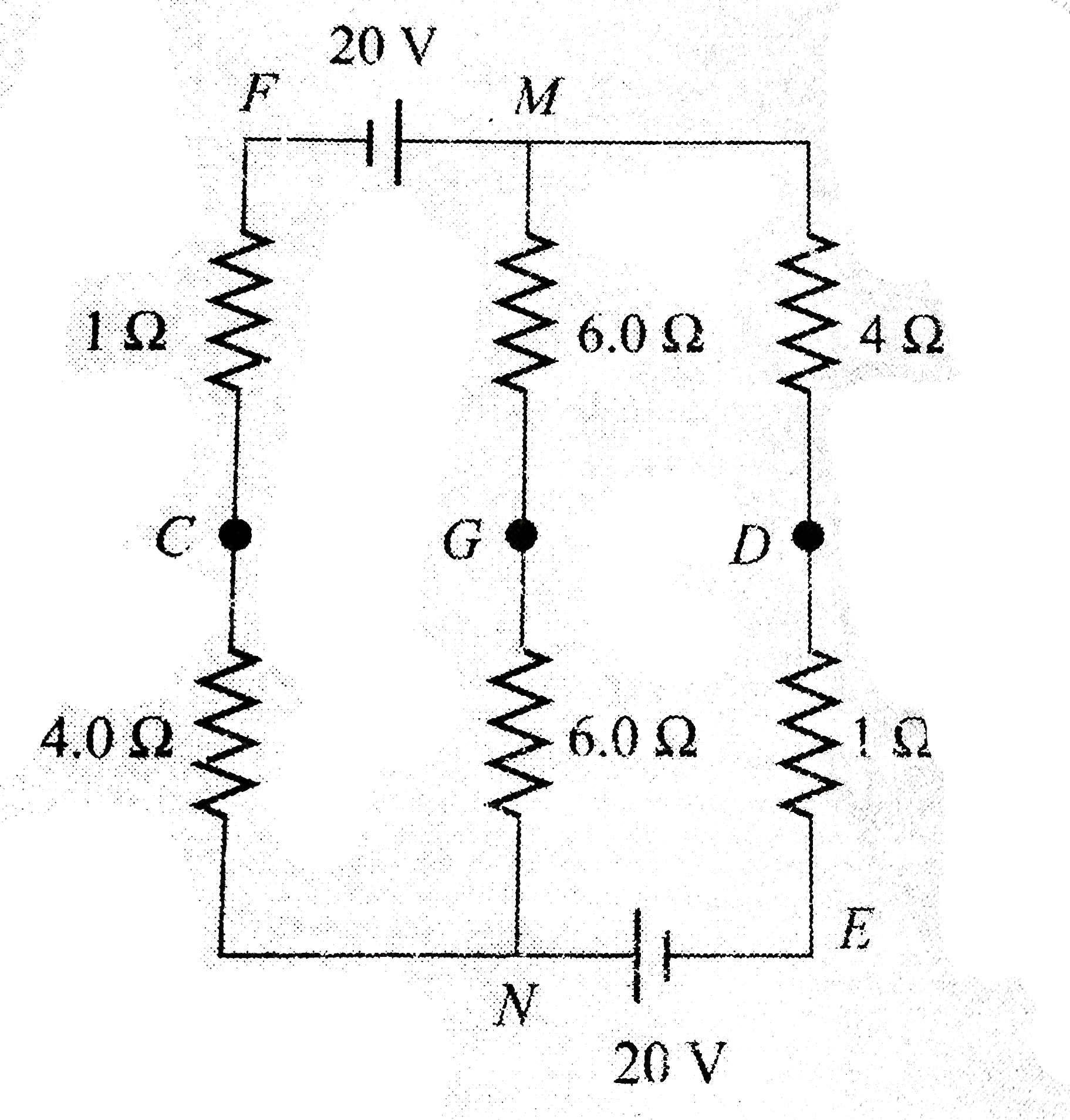
View SolutionThe time constunt of an L−R circuit is 10s. When a resistance of 10ohm is connected in series in a previous circuit, then the time constant becomes. 2s. The self-inductance (in henry) of the circuit is
View SolutionFind current in 10Ω resistance in the circuit shown in figure-3.114.
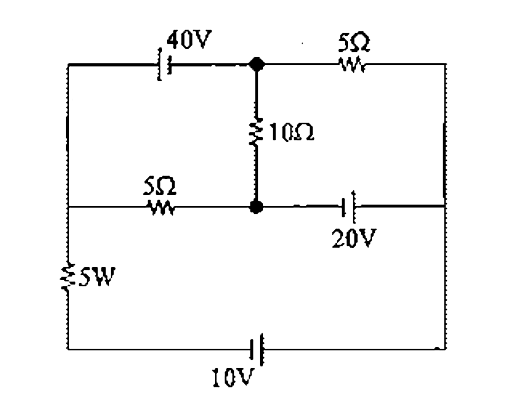
View SolutionIn the circuit, the current flowing through 10Ω resistance
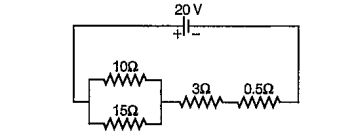
View Solution
