A very small circular loop of area 5×I0−4m2 , resistance 2Ω and negligible inductance is initially coplanar and concentric with a much larger fixed circular loop of radius 0.Im . A constant current of IA is passed in the bigger loop and the smaller loop is rotated with angular velocity ωrad/sec about a diameter. Calculate (a) the flux limked with the smaller loop, (b) indced emf (c) induced current in the smaller loop, as a function of time.
Magnetic field due to large loop at centre
B=μ0i02a (assumed uniform in smaller loop)
Let at any time t , normal to small loop makes angle θ(=ωt) with magnetic field
(a) Flux throuth smaller loop
ϕ=BAcosθ
ϕ=μ0i02aAcosωt
(b) e=−dϕdt=μ0i0Aω2asinωt
(c) I=eR=μ0i0Aω2aRsinωt

Topper's Solved these Questions
Similar Questions
A very small circular loop of radius r is initially coplanar and concentric with a much larger circular loop of radius R(>>r) . A constant current i is passed in the larger loop which is kept fixed in space and the small loop is rotated with angular velocity ω about a diameter. The resistance of the small loop is R0 and the inductance is negligible.
(a) Find the current in the small loop as a function of time.
(b) Calculate how much troque must be exerted on the small loop to rotate it.
View SolutionA very small circular loop of radius a is initially coplanar & concentric with a much larger circular loop of radius b(<<a).A constant current I is passed in the large loop which is kept fixed in space & the small loop is rotated with constant angular velocity ω about a diameter.The resistance of the small loop is R & its inductance is negligible The induced emf in the large loop due to current induced in smaller loop as a function of time is equal to 1x(πa2μ0ωb)2Icos2ωtR.Find out value of x.
View Solution
Knowledge Check
A very small circular loop of radius a is initially (at t = 0) coplanar and concentric with a much larger fixed circular loop of radius b. A constant current I flows in the larger loop. The smaller loop is rotated with a constant angular speed ω about the common diameter. The emf induced in the smaller loop as a function of time t is
Aπa2μ0I2bωcos(ωt)Bπa2μ0I2bωsin(ω2t2)Cπa2μ0I2bωsin(ωt)Dπa2μ0I2bωsin2(ωt)A very small circular loop of radius a is initially (at t = 0) coplanar and concentric with a much larger fixed circular loop of radius b. A constant current I flows in the larger loop. The smaller loop is rotated with a constant angular speed ω about the common diameter. The emf induced in the smaller loop as a function of time t is
Aπa2μ0I2bωcosωtBπa2μ0I2bωsinω2t2Cπa2μ0I2bωsinωtDπa2μ0I2bωsin2ωtA very small circular loop of radius a is initially coplanar & concentric with a much larger circular loop of radius b (>>a). A constant current is passed in the large loop which is kept fixed in space & the small loop is rotated with angular velocity omega about a diameter. The resistance of the small loop is R & its self inductance is negligible. The current in the larger loop is clockwise.
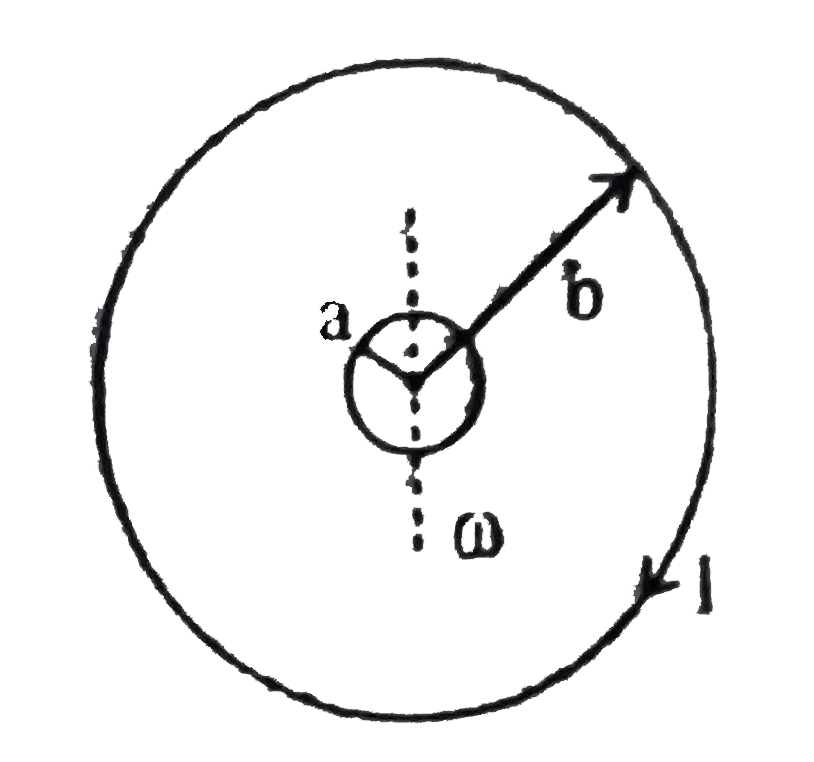
Find the current in the small loop as a function of time.Aπa2μ0Iωsinωt2bRBπa2μ0Iωcosωt2bRCπb2μ0Iωsinωt2aRDπb2μ0Iωcosωt2aR
A very small circular loop of radius a is initially coplanar & concentric with a much larger circular loop of radius b (>>a). A constant current is passed in the large loop which is kept fixed in space & the small loop is rotated with angular velocity omega about a diameter. The resistance of the small loop is R & its self inductance is negligible. The current in the larger loop is clockwise.
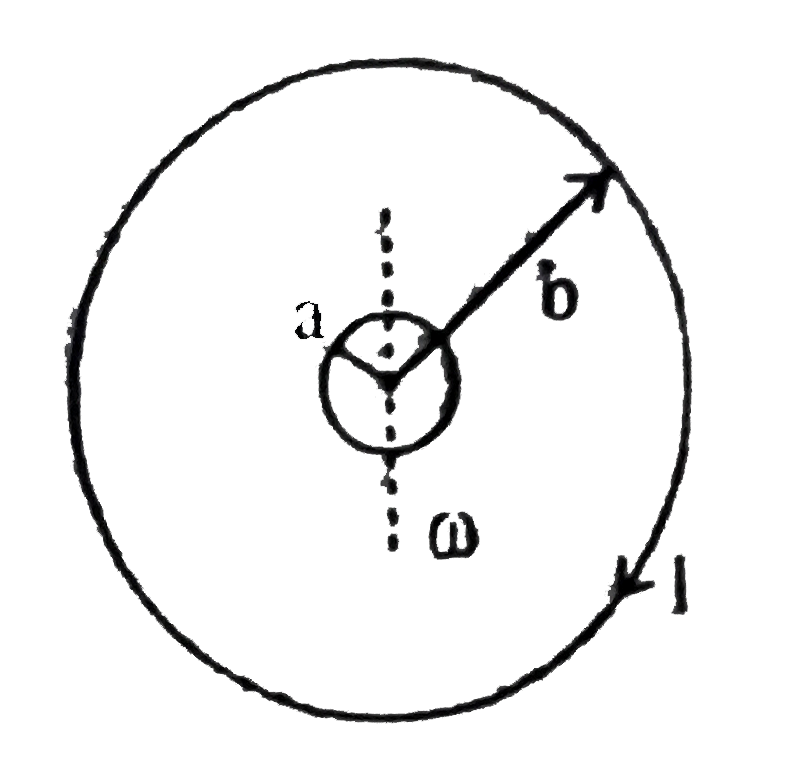
At the moment both the loops are in the same plane
View SolutionA small loop of area of cross -section 10−4m2 is lying concentrically and coplanar inside a bigger loop of radius 0.628m. A current of 10A is passed in the bigger loop. The smaller loop is rotated about its diameter with an angular velocity ω. The magnetic flux linked with the smaller loop will be
View SolutionA very small circular loop of radius a is initially coplanar & concentric with a much larger circular loop of radius b (>>a). A constant current is passed in the large loop which is kept fixed in space & the small loop is rotated with angular velocity omega about a diameter. The resistance of the small loop is R & its self inductance is negligible. The current in the larger loop is clockwise.
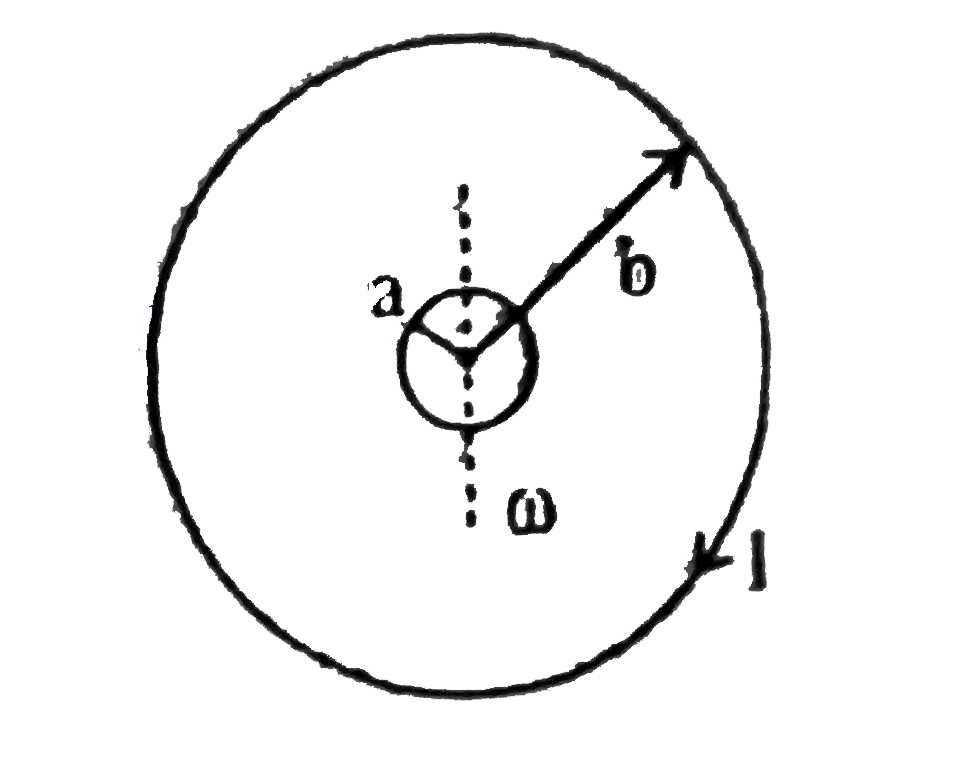
Calculate how much torque must be exerted on the small loop to rotate it.
View SolutionA circular loop of radius 0.05 m carries a current of 1.0 A. The magnetic moment of the loop is .
View SolutionA circular loop of radius0.05 m carriess a current of 1.0 A. The magnetic moment of the loop is .
View Solution
