A 20 mm thick layer of water (n=1.33) floats on a 40 mm thick layer of carbon tetrachloride (n=1.46) in a tank. A coin lies at the bottom of the tank. At what depth below the top water surface do you perceive the coin ?
The correct Answer is:42mm
To solve the problem of determining the perceived depth of the coin lying at the bottom of a tank with two layers of different liquids, we will use the concept of apparent depth and refractive indices.
1. Identify the Layers and Their Properties:
- The top layer is water with a thickness of h1=20mm and a refractive index n1=1.33.
- The bottom layer is carbon tetrachloride (CCl4) with a thickness of h2=40mm and a refractive index n2=1.46.
2. Calculate the Apparent Depth in Each Medium:
- The formula for apparent depth ha in a medium is given by:
ha=hrn
where hr is the real depth and n is the refractive index of the medium.
3. Calculate Apparent Depth for Water:
- For the water layer:
ha1=h1n1=20mm1.33≈15.04mm
4. Calculate Apparent Depth for Carbon Tetrachloride:
- For the carbon tetrachloride layer:
ha2=h2n2=40mm1.46≈27.40mm
5. Total Apparent Depth:
- The total apparent depth ha perceived from the top of the water surface is the sum of the apparent depths from both layers:
ha=ha1+ha2≈15.04mm+27.40mm≈42.44mm
6. Final Result:
- Therefore, the perceived depth of the coin below the top water surface is approximately 42.4mm.
- The top layer is water with a thickness of h1=20mm and a refractive index n1=1.33.
- The bottom layer is carbon tetrachloride (CCl4) with a thickness of h2=40mm and a refractive index n2=1.46.
- The formula for apparent depth ha in a medium is given by:
ha=hrn
where hr is the real depth and n is the refractive index of the medium.
- For the water layer:
ha1=h1n1=20mm1.33≈15.04mm
- For the carbon tetrachloride layer:
ha2=h2n2=40mm1.46≈27.40mm
- The total apparent depth ha perceived from the top of the water surface is the sum of the apparent depths from both layers:
ha=ha1+ha2≈15.04mm+27.40mm≈42.44mm
- Therefore, the perceived depth of the coin below the top water surface is approximately 42.4mm.
Topper's Solved these Questions
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Practice questions(single correct choice type)
49 Videos
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Practice questions(More than one correct choice type)
14 Videos
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Check point
6 Videos
- GEOMETRICAL OPTICS : REFLECTION BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
4 Videos
Similar Questions
In a tank, a 4cm thick layer of water (μ=43) floats on a 6 cm thick layer of an organic liquid (μ = 1.5). Viewing at normal incidence, how far below the water surface does the bottom of tank appear to be?
View SolutionA flat bottomed metal tank filled with water is dragged along a horizontal floor at the rate of 20m/s The tank is of mass 100 kg and contains 900 kg of water and all the heat produced in the dragging is conducted to the water through the bottom plate of the tank. If the bottom plate has an effective area of conduction 1m2 and thickness 5 cm and the temperature of water in the tank remains constant at 50∘ C, calculate the temperature of the bottom surface of the tank. Given the coefficient of friction between the tank and the floor is 0.5 and K for the material of the tank is 100J/msec K.
View Solution
Knowledge Check
Choose the most appropriate option.
A 4cm thick layer of water covers a 6 cm thick glass slab. A coin is placed at the bottom of the slab and is being observed from the air side along the normal to the surface. Find the apparent position of the coin from
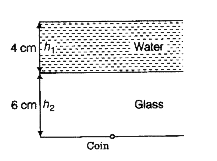 A7.0cmB8.0cmC10 cmD5 cm
A7.0cmB8.0cmC10 cmD5 cmA layer of benzene (μ=1.5) 12 cm thick floats on water layer (μ=4/3) 8 cm thick in a vessel. When viewed from the top, the apparent depth of bottom of vessel below the surface of benzene will be
A20 cmB14 cmC7 cmD21 cmA glass beaker is filled with water up to 5cm. It is kept on top of a 2cm thick glass slab. When a coin at the bottom of the glass slab is viewed at the normal incidence from above the beaker, its apparent depth from the water surface is dcm. Value of d is close (the refractive index of water and glass are 1.33 and 1.50,respectively)
A2.5B5.1C3.7D6
A soap bubble (n=1.33) is floating in air. If the thickness of the bubble wall is 115 nm, what is the wavelength of the light that is most strongly reflected?
View SolutionA tank with vertical walls is monted so that its base is at height of 1.2 m above the horizotnal ground. The tank is filled with water to depth 2.8 m. A holw is punched in the side wall of the tank at a depth x m below the surface of water to have maximum range of the emerging stream. then the value of x in metre is
View SolutionFigure shows a large closed cylindrical tank containing water. Initially, the air trapped above the water surface has a height h0 and pressure 2p0 where rh0 is the atmospheric pressure. There is a hole in the wall of the tank at a depth h1 below the top from which water comes out. A long vertical tube is connected as shown.

Find the height of the water in the long tube above the top when the water stops coming out of the hole.
View SolutionFigure shows a large closed cylindrical tank containing water. Initially, the air trapped above the water surface has a height h0 and pressure 2p0 where rh0 is the atmospheric pressure. There is a hole in the wall of the tank at a depth h1 below the top from which water comes out. A long vertical tube is connected as shown.

Find the height h2 of the water in the long tube above top initially.
View SolutionA solid glass hemisphere of density d and radius R lies (with curved surface of hemisphere below the flat surface) at the bottom of a tank filled with water of density ρ such that the flat surface of hemisphere is H depth below the liquid surface. Weight of water + tank is W1 and that of hemisphere is'W2. W Then choose the incorrect options
View Solution
