In a tank, a 4cm thick layer of water floats on a 6 cm thick layer of an organic liquid ( = 1.5). Viewing at normal incidence, how far below the water surface does the bottom of tank appear to be?
To solve the problem, we need to determine how far below the water surface the bottom of the tank appears to be when viewed from above. We will use the concept of apparent depth, which takes into account the refractive indices of the fluids involved.
1. Identify the Given Data:
- Thickness of water layer, tw=4cm
- Refractive index of water, μw=43
- Thickness of organic liquid layer, to=6cm
- Refractive index of organic liquid, μo=1.5
- Refractive index of air, μ=1
2. Use the Formula for Apparent Depth:
The formula for the apparent depth d when viewing through multiple layers is given by:
d=twμw+toμo
where tw and to are the thicknesses of the water and organic liquid layers, respectively, and μw and μo are their respective refractive indices.
3. Calculate the Contributions from Each Layer:
- For the water layer:
Contribution from water=twμw=4cm43=4×34=3cm
- For the organic liquid layer:
Contribution from organic liquid=toμo=6cm1.5=4cm
4. Sum the Contributions:
Now, we add the contributions from both layers to find the total apparent depth:
d=3cm+4cm=7cm
5. Conclusion:
Therefore, the bottom of the tank appears to be 7cm below the water surface.
Final Answer:
The bottom of the tank appears to be 7 cm below the water surface.
- Thickness of water layer, tw=4cm
- Refractive index of water, μw=43
- Thickness of organic liquid layer, to=6cm
- Refractive index of organic liquid, μo=1.5
- Refractive index of air, μ=1
The formula for the apparent depth d when viewing through multiple layers is given by:
d=twμw+toμo
where tw and to are the thicknesses of the water and organic liquid layers, respectively, and μw and μo are their respective refractive indices.
- For the water layer:
Contribution from water=twμw=4cm43=4×34=3cm
- For the organic liquid layer:
Contribution from organic liquid=toμo=6cm1.5=4cm
Now, we add the contributions from both layers to find the total apparent depth:
d=3cm+4cm=7cm
Therefore, the bottom of the tank appears to be 7cm below the water surface.
The bottom of the tank appears to be 7 cm below the water surface.
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - CUQ (REFLECTION)
9 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - CUQ (REFRECTION)
28 Videos
- NUCLEI BOOK - NARAYNACHAPTER - NUCLEI EXERCISE - ASSERTION & REASON
5 Videos
- SEMI CONDUCTOR DEVICESBOOK - NARAYNACHAPTER - SEMI CONDUCTOR DEVICESEXERCISE - Level-II (H.W)
36 Videos
Similar Questions
A 20 mm thick layer of water (n=1.33) floats on a 40 mm thick layer of carbon tetrachloride (n=1.46) in a tank. A coin lies at the bottom of the tank. At what depth below the top water surface do you perceive the coin ?
View SolutionThe number of waves in a 3 - cm- thick layer of a liquid is same as in 4 - cm - thick layer of another liquid. If the refractive index of the first liquid is 1.8, then what will be for that of another liquid?
View Solution
Knowledge Check
Choose the most appropriate option.
A 4cm thick layer of water covers a 6 cm thick glass slab. A coin is placed at the bottom of the slab and is being observed from the air side along the normal to the surface. Find the apparent position of the coin from
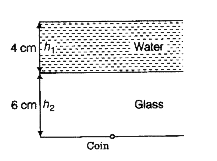 A7.0cmB8.0cmC10 cmD5 cm
A7.0cmB8.0cmC10 cmD5 cmA rectangular tank of depth 8 m is full of water (μ=4/3). The bottom is seen at the depth
A6 cmB83 cmC8 cmD10 cmA layer of benzene (μ=1.5) 12 cm thick floats on water layer (μ=4/3) 8 cm thick in a vessel. When viewed from the top, the apparent depth of bottom of vessel below the surface of benzene will be
A20 cmB14 cmC7 cmD21 cm
A wide vessel of uniform cross-section with a small hole in the bottom is filled with "40cm thick layer of water and "30cm" thick layer of kerosene.The relative density of kerosene is "],[0.8" .The initial velocity of flow of water streaming out of the hole is (take g=10ms−2
View SolutionA wide vessel of uniform cross- section with a small hole in the bottom is filled with 40cm thick layer of water and 30cm thick layer of kerosene.The relative density of kerosene is 0.8 .The initial velocity of flow of water streaming out of the hole is (take g=10ms−2 )
View SolutionThe bottom of a container is a 4.0 cm thick glass (μ=1.5) slab. The container contains two immiscible liquids A and B of depth 6.0 cm and 8.0 cm respectively. What is the apparent position of a scratch on the outer surface of the bottom of the glass slab when viewed through the container? Refractive indices of A and B are 1.4 and 1.3 respectively.
View SolutionThe height of the water in a tank is H. The range of the liquid emerging out from a hole in the wall of the tank at a depth 3H4 from the upper surface of water, will be
View SolutionA glass prism (μ=1.5) is dipped in water (μ=4/3) as shown in figure. A light ray is incident normally on the surface AB . It reaches the surface BC after totally reflected, if
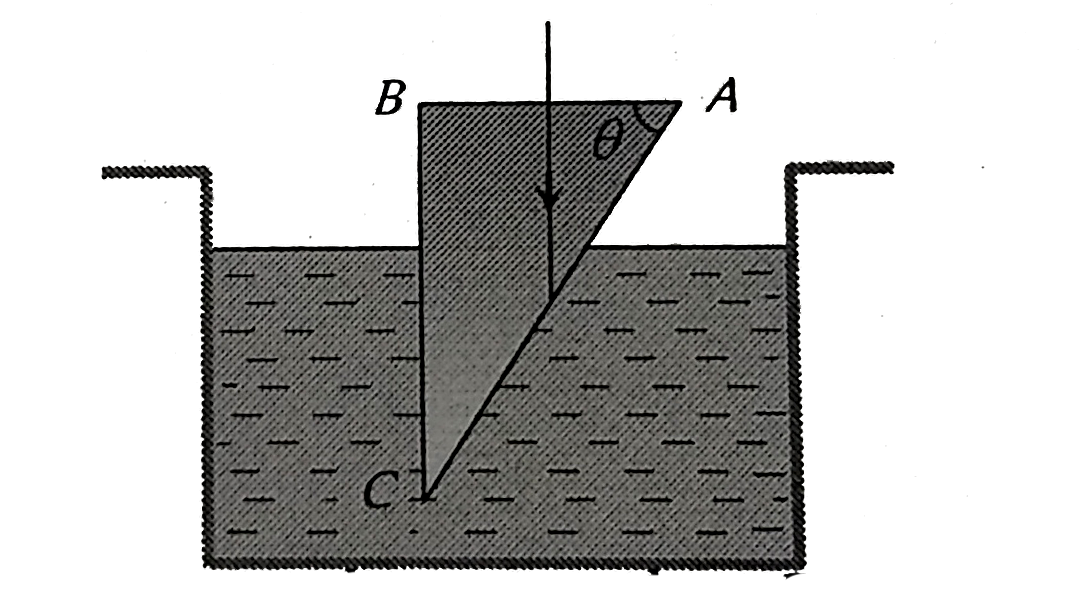
View Solution
