Two large metal sheets carry surface currents as shown in figure . The current through a strip of width dl is Kdl where K is a constant . Find the magnetic field at the points P,Q and R.

(1) This situation has planar symmetry, so we expect that, in analogy to the electric field of a flat charged sheet, the field on either side of the plate is uniform. That is to say,
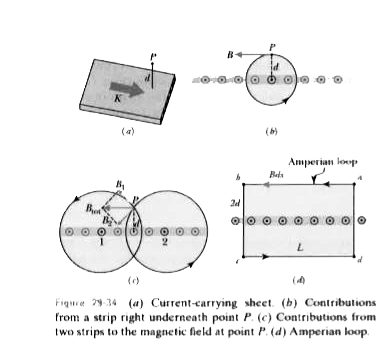
the magnitude and direction of the magnetic field does not depend on the distance from the plane. Before we can use Ampere.s law to verify this dependence, we must determine the direction of the magnetic field at an arbitrary point P above the charged sheet.
(2) We divide the sheet into thin parallel strips in the direction of the current. We then treat each strip as a current-carrying wire. A cross-sectional view of the sheet, looking into a direction opposite that of the current through the sheet, is shown in Fig. 29-34b. Using the right-hand rule, we find that the strip right underneath point P contrubutes a magnetic field that points parallel to the plate and to the left. Next, we look at the contrubutions from two stripes, 1 and 2, equidistant on either side of P (see Fig.29-34c).The two circles show the field lines from either strip that go through P. The magnitudes of the contributions from the two strips are equal and so we see that the sum of the contributions from these two strips also point parallel to the plate and to the left . Arguing this way, we can say that the entire magnetic field due to the sheet is parallel to the sheet and points to the left. Calculation : To use this fact in Ampere.s law, we choose the rectangular loop abcd as shown in Fig.29-34d as the Amperian loop. The width of this rectangular loop is L and its height is 2d. The line integral around the loop can then be written as the sum of four line integrals over each side of the rectangle.
∮→B⋅d→s=∫ba→B⋅d→s+∫cb→B⋅d→s+∫dc→B⋅d→s+∫ad→B⋅d→s
Along the vertical sides bc and da, the magnetic field is perpendicular to the path and so the dot product →B⋅d→s is zero . Over the other two sides the magnetic field is parallel to the path and so →B⋅d→s=Bds.
Symmetry dicates that the magnitude of the magnetic field a distance d below the sheet is the same as that a distance d above it (because flipping the plane upside down should not alter the physical situation) and so we can take this magnitude, B out of the integral, that is
∮→B⋅d→s=∫abBds+∫cdBds=B∫abds+B∫cdds
The two remaining line integrals simply yield the lengths of the two sides and so the left hand side of Ampere.s law becomes
∮→B⋅d→s=B(2L)=2BL
Substituting for the right hand side of Eq. (29-42) into Ampere.s law we get
2BL=μ0KL
B=12μ0K
Conclude : So we see that the magnetic field does not depend on the distance to the plane just like the electric field of a large uniformly charged sheet.
Topper's Solved these Questions
- MAGNETIC FIELDS DUE TO CURRENTSBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Check point
4 Videos
- MAGNETIC FIELDS DUE TO CURRENTSBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FIELDS DUE TO CURRENTSEXERCISE - Problems
45 Videos
- INTERFERENCE AND DIFFRACTION BOOK - RESNICK AND HALLIDAYCHAPTER - INTERFERENCE AND DIFFRACTION EXERCISE - PRACTICE QUESTIONS (Integer Type)
6 Videos
- MAGNETIC FORCEBOOK - RESNICK AND HALLIDAYCHAPTER - MAGNETIC FORCEEXERCISE - Practice Questions (Integer type )
7 Videos
Similar Questions
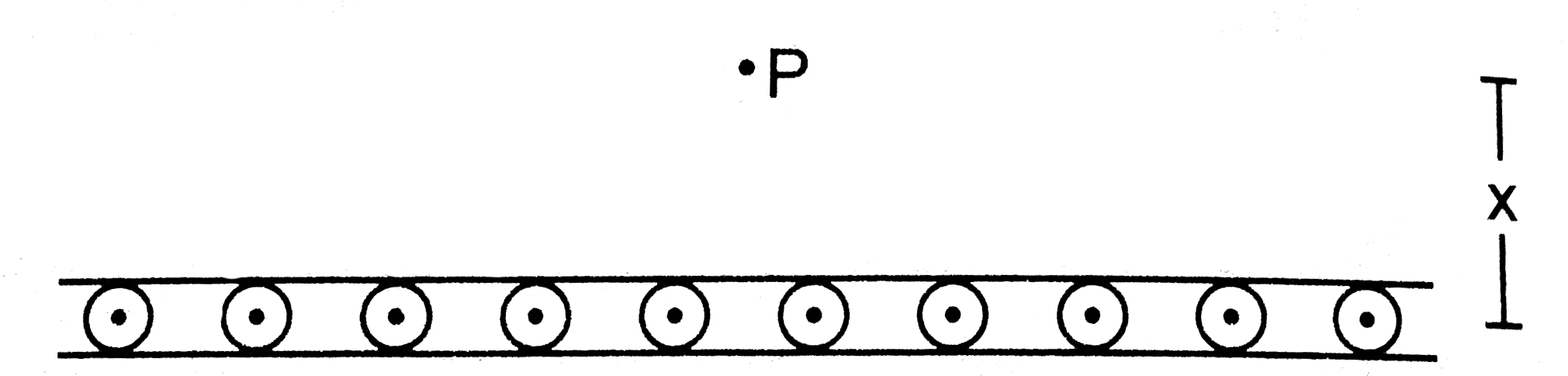
Figure shows a cross section of a large metal. Sheet carrying an electric current along its surface. The current in a strip of width dl is Kdl where K is a constant. Find the magnetic field at a point P at a distance x from the metal sheet.
View SolutionA long cylidrical conductor of radius R carries a current i as shown in figure. The current desity J is a function of radius according to J=br, where b is a constant. Find an expression for the magnetic field B

a. at a distasnce r1<R and
b.at a distance r2>R, measured from the axis.
View Solution
Knowledge Check
A coil having N turns carry a current I as shown in the figure. The magnetic field intensity at point P is
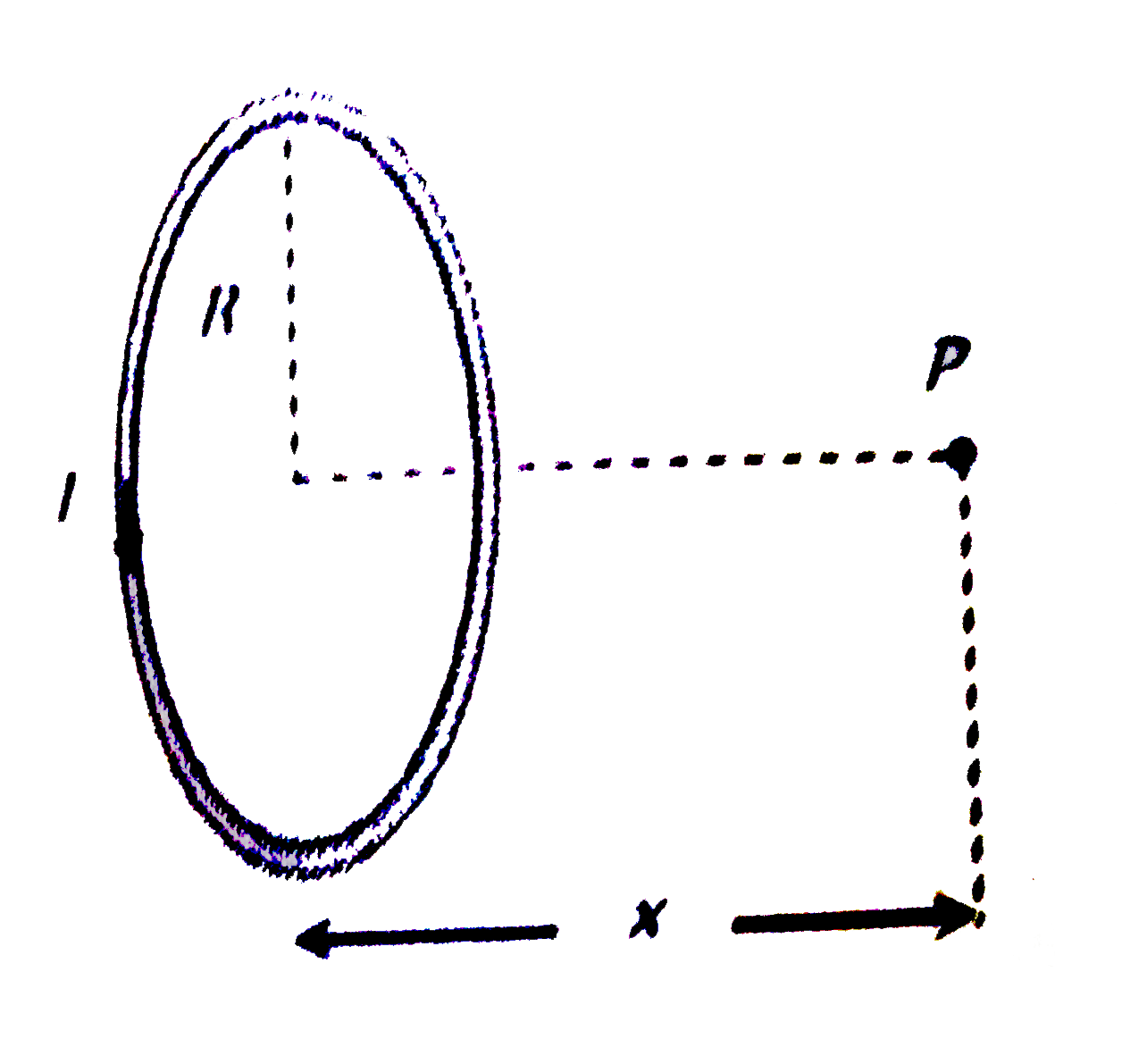 Aμ0NIR22(R2+x2)3/2Bμ0NI2RCμ0NIR2(R+x)2DZero
Aμ0NIR22(R2+x2)3/2Bμ0NI2RCμ0NIR2(R+x)2DZeroShown in the figure is a conductor carrying a current i. the magnetic field at the origin is :
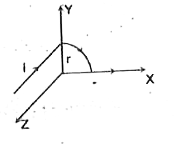 Aμ0i4r(ˆiπ+ˆj2)B−μ0i4r(ˆiπ+ˆk2)Cμ0i4r(ˆi2+ˆiπ)Dμ0i4r(2ˆiπ+ˆj)
Aμ0i4r(ˆiπ+ˆj2)B−μ0i4r(ˆiπ+ˆk2)Cμ0i4r(ˆi2+ˆiπ)Dμ0i4r(2ˆiπ+ˆj)
A tightly- wound, long solenoid is kept with its axis parallel to a large metal sheet carrying a surface current. The surgace current through a width dl of the sheet is Kdl and the number of turns per unit length of the solenoid is n. The magnetic field near the centre of the solenoid is found to be zero. (a) find the current in the solenoid. (b) If the solenoid is rotated to make its axis perpendicular to the metal sheet, what would be the magnitude of the magnetic field near its centre?
View SolutionFig shows two current-carrying wires 1 and 2. Find the magnitudes and directions of the magnetic field at points P,Q and R.

View SolutionA long cylindrical conductor of radius R carries a current i as shown in the figure. The current density J varies across the cross-section as J=kr2, where, k is a constant. Find an expression for the magnetic field B at a distance r(<R) from the axis

View SolutionShown in Fig. is a conductor carrying current I. Find the magnetic field intensity at point O.
View SolutionThere are two parallel current carrying wires X and Y as shown in figure. Find the magnitude and direction of the magnetic field at points, P, Q and R.
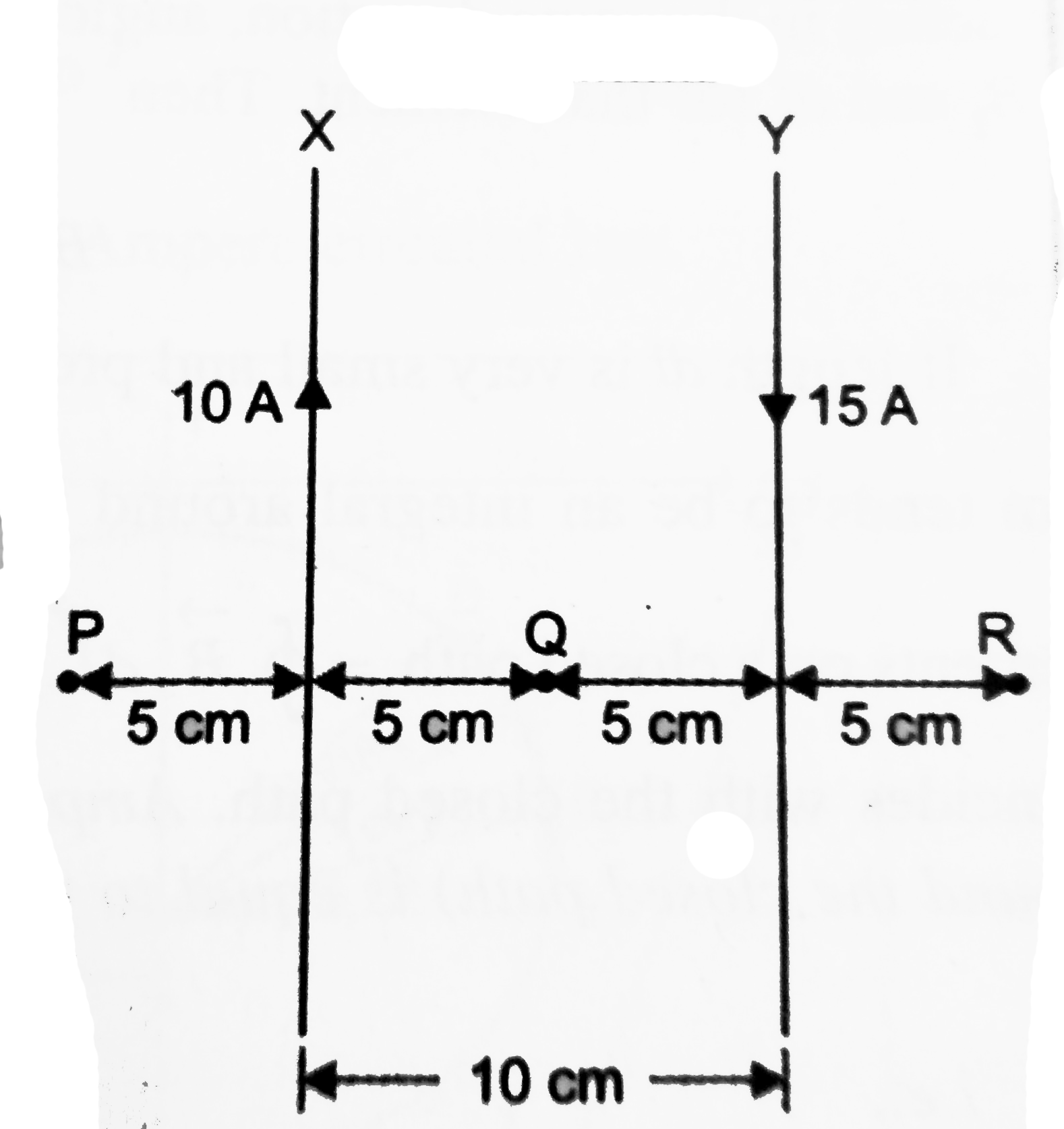
View SolutionTwo infinite plates shown in cross-section in figure carry λ amperes of current out of thepage per unit width of plate. Find the magnetic field at points P and Q.

View Solution
