A violin string 15.0 cm long and fixed at both ends oscillates in its N = 1 mode. The speed of waves on the string is 280 m/s, and the speed of sound in air is 318 m/s. What are the (a) frequency and (b) wavelength of the emitted sound wave?
To solve the problem step by step, we need to find the frequency and wavelength of the emitted sound wave from a violin string that is oscillating in its fundamental mode (N = 1).
Step 1: Determine the Wavelength of the String Vibration
The length of the violin string is given as L=15.0cm=0.15m.
In the fundamental mode (N = 1), the relationship between the wavelength (λ) and the length of the string is given by:
λ2=L
Substituting the length of the string:
λ2=0.15m
To find λ:
λ=2×0.15m=0.30m
Step 2: Calculate the Frequency of the String Vibration
The speed of the wave on the string is given as v=280m/s.
The frequency (f) can be calculated using the formula:
f=vλ
Substituting the values:
f=280m/s0.30m=933.33Hz
Step 3: Determine the Wavelength of the Emitted Sound Wave
The speed of sound in air is given as vair=318m/s.
Since the frequency of the sound wave emitted will be the same as the frequency of the string vibration, we use the same frequency calculated:
f=933.33Hz
Now, we can find the wavelength of the emitted sound wave using the formula:
λsound=vairf
Substituting the values:
λsound=318m/s933.33Hz≈0.34m
Final Answers
(a) The frequency of the emitted sound wave is approximately 933.33Hz.
(b) The wavelength of the emitted sound wave is approximately 0.34m.
---
Topper's Solved these Questions
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
35 Videos
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
6 Videos
- WAVE - IIBOOK - RESNICK AND HALLIDAYCHAPTER - WAVE - IIEXERCISE - CHECKPOINTS
4 Videos
- VECTORS BOOK - RESNICK AND HALLIDAYCHAPTER - VECTORS EXERCISE - PRACTICE QUESTIONS
39 Videos
- WAVES-IBOOK - RESNICK AND HALLIDAYCHAPTER - WAVES-IEXERCISE - Practice Questions (Integer Type)
4 Videos
Similar Questions
A sound source A and a reflecting surface B move directly toward each other. Relative to the air, the speed of source A is 20.0 m/s, the speed of surface B is 80.0 m/s, and the speed of sound is 329 m/s. The source emits waves at frequency 2000 Hz as measured in the source frame. In the reflector frame, what are the (a) frequency and (b) wavelength of the arriving sound waves? In the source frame, what are the (c) frequency and (d) wavelength of the sound waves reflected back to the source?
View SolutionThe speed of sound waves in air at 300K is 332 m/s. At what temperature will the speed be 574 m/s
View Solution
Knowledge Check
The speed of sound in air at NTP is 332 m/s. If air pressure becomes four times the normal then the speed of sound waves will :
ADoubleBQuadrupleCRemain the sameDbecome 14 of the original valueA string fixed at both ends oscillates in 5 segments, length 10 m and velocity of wave is 20 ms−1. What is the frequency?
A5 HzB15 HzC10 HzD2 HzFrequency of audible sound waves ranges between 20 Hz and 20 KHz. If the velocity of sound in air is 320 m/s, the range of the wavelengths of the sound in air is
A1.6 cm to 16 mB1.6 m to 16 mC16 cm to 16 mD16 mm to 16 m
The speed of sound waves in air at 300K is 332 m/s. At what temperature will the speed be 574 m/s
View SolutionA 2 m-long string fixed at both ends is set into vibrations in its first overtone. The wave speed on the string is 200 m s and the amplitude is 0.5 cm. (a) Find the wavelength and the frequency. (b) Write the equation giving the displacement of different points as a function of time. Choose the X-axis along the string with the origin at one end and t = 0 at the instant when the point x= 50 cm has reached its maximum displacement.
View SolutionFor the wave shown in the figure, the frequency and wavelength if its speed is 320 m/s are
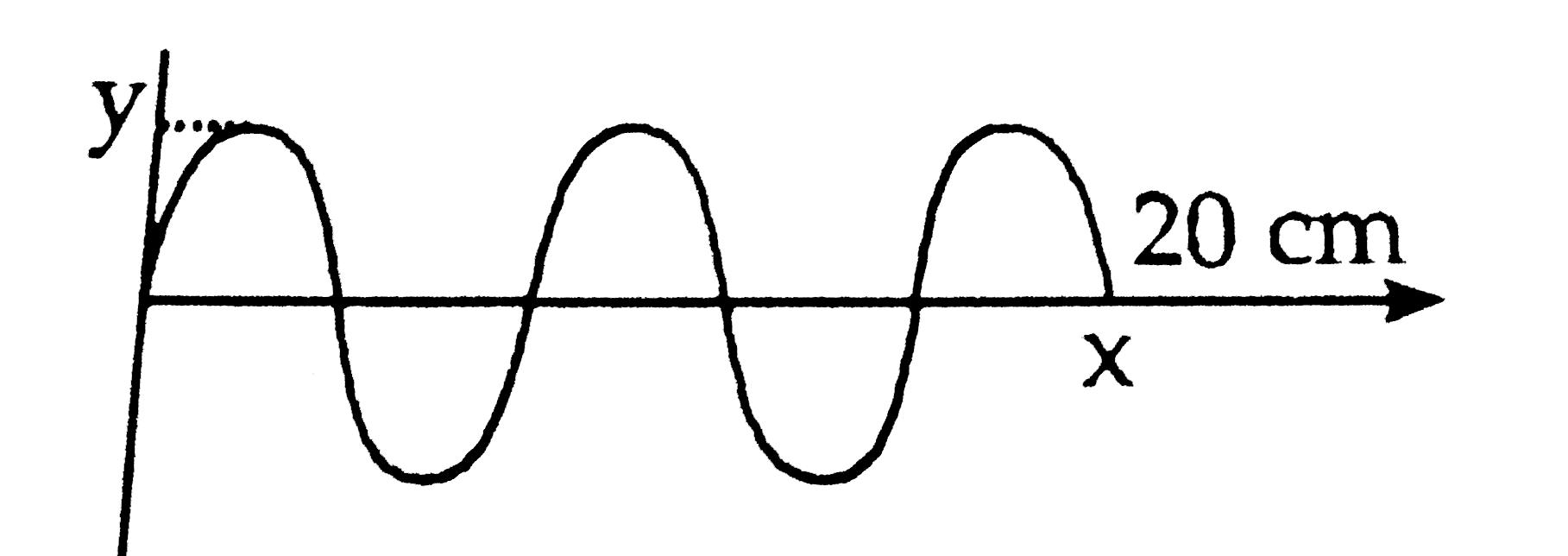
View SolutionA source of sound of frequency 1000 Hz moves to the right with a speef of 32ms relative to the ground. To its right there is a reflecting surface moving to the left with a speed of 64ms relative to the ground. Take the speed of 64ms. Relative to the ground. Take the speed of sound in air to be 332ms and find
(a) The wavelength of the sound emitted in air by the source,
(b) the number of waves per second arriving at the reflecting surface, (c ) The speed of the reflected waves and
(d) The wavelength of the reflected waves.
View SolutionA fire whistle emits a tone of 170 Hz. Take the speed of sound in air to be 340 m/s. The wavelength of this sound is about
View Solution
