Two sounds differ in sound level by 3.00 dB. What is the ratio of the greater intensity to the smaller intensity?
To solve the problem of finding the ratio of the greater intensity to the smaller intensity when two sounds differ in sound level by 3.00 dB, we can follow these steps:
Step 1: Understand the Decibel Formula
The sound level in decibels (dB) is given by the formula:
L=10log10(II0)
where L is the sound level in dB, I is the intensity of the sound, and I0 is the reference intensity (the threshold of hearing).
Step 2: Set Up the Equations for Two Sound Levels
Let L1 be the sound level of the greater intensity IG and L2 be the sound level of the smaller intensity IS. According to the formula, we can write:
L1=10log10(IGI0)(1)
L2=10log10(ISI0)(2)
Step 3: Use the Given Difference in Sound Levels
We know that the difference in sound levels is given as:
L1−L2=3dB
Substituting equations (1) and (2) into this, we have:
10log10(IGI0)−10log10(ISI0)=3
Step 4: Simplify the Equation
Using the properties of logarithms, we can simplify the left side:
10(log10(IGI0)−log10(ISI0))=3
This simplifies to:
10log10(IGIS)=3
Dividing both sides by 10 gives:
log10(IGIS)=0.3
Step 5: Convert Logarithmic Form to Exponential Form
To find the ratio of the intensities, we take the antilogarithm:
IGIS=100.3
Step 6: Calculate the Value of the Ratio
Calculating 100.3:
100.3≈2
Thus, the ratio of the greater intensity to the smaller intensity is:
IGIS≈2
Final Answer
The ratio of the greater intensity to the smaller intensity is approximately 2.
---
The sound level in decibels (dB) is given by the formula:
L=10log10(II0)
where L is the sound level in dB, I is the intensity of the sound, and I0 is the reference intensity (the threshold of hearing).
Let L1 be the sound level of the greater intensity IG and L2 be the sound level of the smaller intensity IS. According to the formula, we can write:
L1=10log10(IGI0)(1)
L2=10log10(ISI0)(2)
We know that the difference in sound levels is given as:
L1−L2=3dB
Substituting equations (1) and (2) into this, we have:
10log10(IGI0)−10log10(ISI0)=3
Using the properties of logarithms, we can simplify the left side:
10(log10(IGI0)−log10(ISI0))=3
This simplifies to:
10log10(IGIS)=3
Dividing both sides by 10 gives:
log10(IGIS)=0.3
To find the ratio of the intensities, we take the antilogarithm:
IGIS=100.3
Calculating 100.3:
100.3≈2
Thus, the ratio of the greater intensity to the smaller intensity is:
IGIS≈2
The ratio of the greater intensity to the smaller intensity is approximately 2.
Topper's Solved these Questions
- WAVE - IIBook:RESNICK AND HALLIDAYChapter:WAVE - IIExercise:PRACTICE QUESTIONS (SINGLE CORRECT CHOICE TYPE)
Explore 35 Videos
- WAVE - IIBook:RESNICK AND HALLIDAYChapter:WAVE - IIExercise:PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
Explore 6 Videos
- WAVE - IIBook:RESNICK AND HALLIDAYChapter:WAVE - IIExercise:CHECKPOINTS
Explore 4 Videos
- VECTORS Book:RESNICK AND HALLIDAYChapter:VECTORS Exercise:PRACTICE QUESTIONS
Explore 39 Videos
- WAVES-IBook:RESNICK AND HALLIDAYChapter:WAVES-IExercise:Practice Questions (Integer Type)
Explore 4 Videos
Similar Questions
Many veteran rockers suffer from acute hearing damage because of the high sound levels they endured for years. Many rockers now wear special earplugs to protect their hearing during performances . If an earplug decreases the sound level of the sound waves by 20 dB, what is the ratio of the final intensity If of the waves to their initial intensity Ii ?
View SolutionTwo sound waves from two different sources interfere at a point to yield a sound of varying intensity. The intensity level between the maximum and minimum is 20 dB. What is the ratio of the intensities of the individual waves?
View Solution
Knowledge Check
Two sounds in a gas differ in their loudness level by 20 db. What is the ratio of the amplitudes of the pressure oscillations ?
A10:1B104:1C√10:1D100:1Intensity of sound wave is
Aequal to product of energy density and wave velocityBproportional to the square of the frequencyCproportional to the wave velocityDall of the aboveThe intensity level of two sounds are 100 dB and 50 dB. What is the ratio of their intensities?
A101B103C105D1010
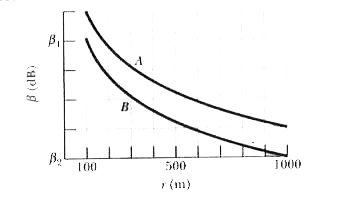
Two atmospheric sound sources A and B emit isotropically at constant power. The sound levels β of their emissions are plotted in Fig. versus the radial distance r from the sources. The vertical axis scale is set by β1=85.0dBandβ2=65.0dB . What are (a) the ratio of the larger power to the smaller power and (b) the sound level difference at r = 23 m?
View SolutionFour souces of sound each of sound level 10dB are sounded together in phase, the resultant intensity level will be (110/n) dB. Find value of n (log102=0.3).
View SolutionA certain sound source is increased in sound level by 40.0 dB. By what multiple is (a) its intensity increased and (b) its pressure amplitude increased?
View SolutionIdentify the unit of measuring intensity of sound
View SolutionFour sources of sound each of sound level 10dB are sounded together in phase , the resultant intensity level will be (log102=0.3)
View Solution