A man swims across the river which flows with a velocity of 3 km/h due east. If the velocity of man relative to water is 4 km/h due north, then what is his velocity and its direction relative to the shore of the river?
4 km/h, 63∘50' west of north
5 km/h, 36∘52' west of north
4 km/h, 63∘50' east of north
5 km/h, 36∘52' east of north
The correct Answer is:D
To solve the problem of finding the man's velocity relative to the shore of the river, we can break it down into a few steps:
Step 1: Identify the velocities
- The velocity of the river (V_r) is 3 km/h due east. In vector form, this can be represented as:
Vr=3^i km/h
- The velocity of the man relative to the water (V_mw) is 4 km/h due north. In vector form, this can be represented as:
Vmw=4^j km/h
Step 2: Determine the man's velocity relative to the ground
To find the man's velocity relative to the ground (V_m), we can use vector addition:
Vm=Vmw+Vr
Substituting the values:
Vm=4^j+3^i
Step 3: Calculate the magnitude of the resultant velocity
The magnitude of the resultant velocity can be calculated using the Pythagorean theorem:
|Vm|=√(Vmx)2+(Vmy)2
Where Vmx=3 km/h and Vmy=4 km/h:
|Vm|=√(3)2+(4)2=√9+16=√25=5 km/h
Step 4: Determine the direction of the resultant velocity
To find the direction, we can use the tangent function:
tan(θ)=VmyVmx=43
Thus,
θ=tan−1(43)
Calculating this gives:
θ≈53.13∘
This angle is measured from the east towards the north.
Step 5: State the final answer
The man's velocity relative to the shore of the river is:
- Magnitude: 5 km/h
- Direction: 53.13° north of east.
Summary
The final answer is:
- Velocity: 5 km/h
- Direction: 53.13° north of east.
- The velocity of the river (V_r) is 3 km/h due east. In vector form, this can be represented as:
Vr=3^i km/h
- The velocity of the man relative to the water (V_mw) is 4 km/h due north. In vector form, this can be represented as:
Vmw=4^j km/h
To find the man's velocity relative to the ground (V_m), we can use vector addition:
Vm=Vmw+Vr
Substituting the values:
Vm=4^j+3^i
The magnitude of the resultant velocity can be calculated using the Pythagorean theorem:
|Vm|=√(Vmx)2+(Vmy)2
Where Vmx=3 km/h and Vmy=4 km/h:
|Vm|=√(3)2+(4)2=√9+16=√25=5 km/h
To find the direction, we can use the tangent function:
tan(θ)=VmyVmx=43
Thus,
θ=tan−1(43)
Calculating this gives:
θ≈53.13∘
This angle is measured from the east towards the north.
The man's velocity relative to the shore of the river is:
- Magnitude: 5 km/h
- Direction: 53.13° north of east.
The final answer is:
- Velocity: 5 km/h
- Direction: 53.13° north of east.
Topper's Solved these Questions
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
3 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (LINKED COMPREHENSION)
14 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PROBLEMS
50 Videos
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )
3 Videos
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions
57 Videos
Similar Questions
A river flows due south with a speed of 2.0ms−1. A man strees a motorboat across the river , his velocity relative to the water is 4ms−1 due east. The river is 800m wide.
(a) What is his velocity (magnitude and direction) relative to the earth ?
(b) How much time is required to cross the river ?
( c) HOw far south of his starting points will he reach the opposite bank ?
View SolutionA train is moving with a velocity of 30kmh−1 due East and a car is moving with a veloicty of 40kmh−1 due North . What is the velocity of car as appears to a passenger in the train ?
View Solution
Knowledge Check
A boat crosses a river with a velocity of 8kmh. If the resulting velocity of boat is 10kmh then the velocity of river water is
A4kmhB6kmhC8kmhD10kmhAt a harbour, a boat is standing and wind is blowing at a speed of √2m/sec. due to which , the flag on the boat flutters along north− east. Now the boat enters in to river, which is flowing with a velocity of 2m/sec. Due north. The boat starts with zero velocity relative to the river and its constant acceleration relative to the river is 0.2m/sec2 due east. In which direction will the flag flutter at 10 seconds ?
Asouth−eastBsouth−westC30∘south of westDwestA man swims to and fro along the bank of a river with a velocity v relative to water. If the velocity of flow is u, the average speed of the man (for to and fro motion) is :
A0B√uvCu+v2Dv2−u2v
A train is moving with a velocity 40kmh−1 due East and a car is moving with a velocity 60kmh−10 due North, What is the velocity of train as appears to a passenger in the car ?
View SolutionA man going east in a car with a velocity of 20 km/hr, a train appears to him to move towards north with a velocity of 20√3 km/hr. What is the actual velocity and direction of motion of train?
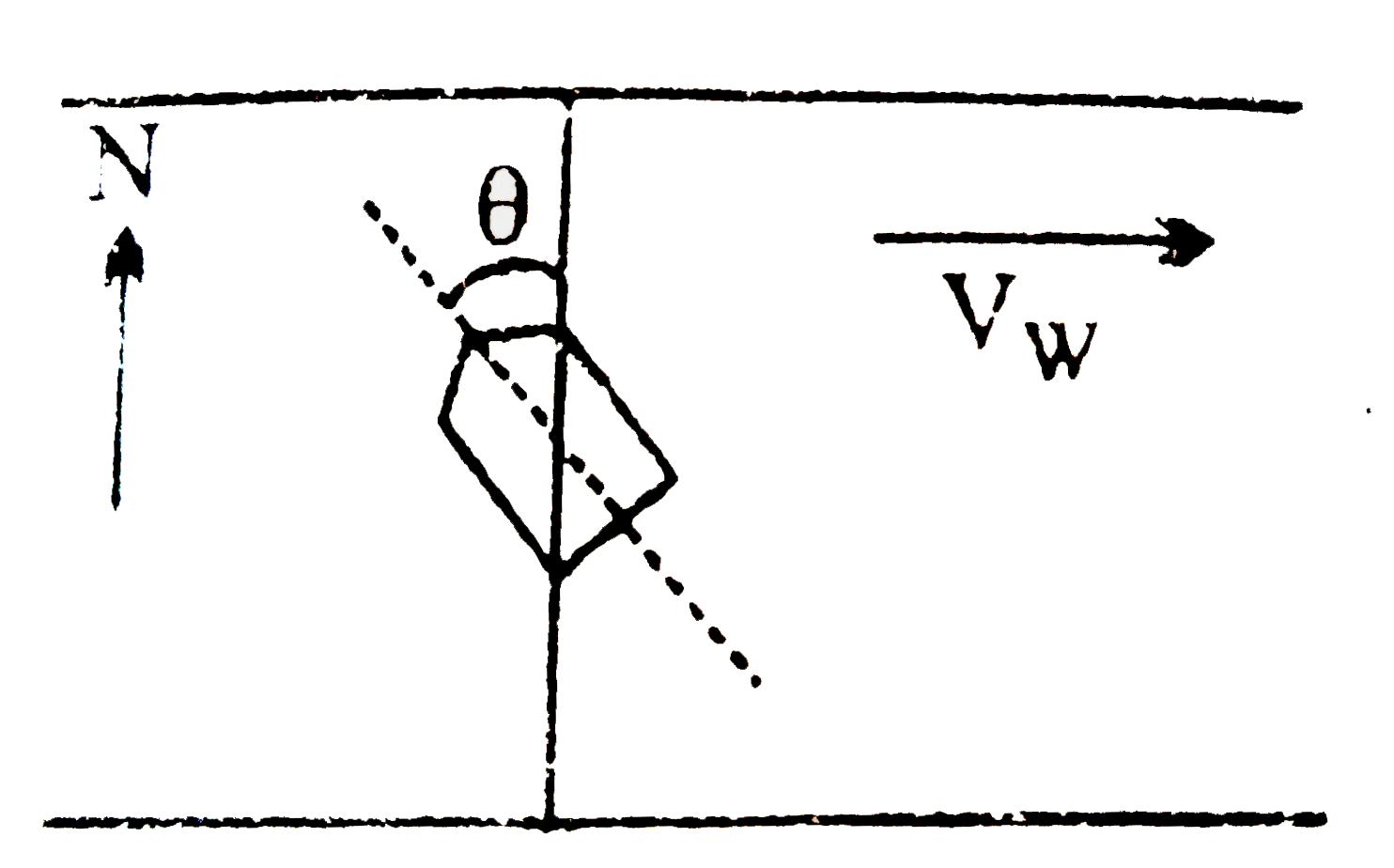
View SolutionA boat is to go straight across a stream that is flowing at 5.0 km/h to east. The boatman knows that his speed with respect to water is 10 km/h. the angle θ at which he must head the boat, and his speed relative to the shore will be
View SolutionA man in swimming with the uniform velocity of 6km/h straight across a river which is flowing at the rate of 2km/h. If the breadth of the river is 300 m, the distance between the point and the man is initially directed to and the point it will reach on the opposite bank of the river is equal to :
View SolutionA man in swimming with the uniform velocity of 6km/h straight across a river which is flowing at the rate of 2km/h. If the breadth of the river is 300 m, the distance between the point and the man is initially directed to and the point it will reach on the opposite bank of the river is equal to :
View Solution
