A bullet is fired from a rifle that is held 1.6 m above the ground in a horizontal position. The initial speed of the bullet is 1100 m/s. Find the time it takes for the bullet to strike the ground and the horizontal distance traveled by the bullet.
0.24 s, 693 m
0.57 s, 630 m
0.32 s, 440 m
0.63 s, 352 m
The correct Answer is:B
To solve the problem, we need to break it down into two parts: finding the time it takes for the bullet to strike the ground and then calculating the horizontal distance traveled by the bullet.
Step 1: Calculate the time to strike the ground
1. Identify the known values:
- Height (h) = 1.6 m (the bullet is fired from this height)
- Initial vertical velocity (u) = 0 m/s (the bullet is fired horizontally)
- Acceleration due to gravity (a) = -9.8 m/s² (downward)
2. Use the second equation of motion:
The equation we will use is:
h=ut+12at2
Substituting the known values into the equation:
−1.6=0⋅t+12(−9.8)t2
This simplifies to:
−1.6=−4.9t2
3. Solve for t²:
Rearranging gives:
t2=1.64.9
Calculating this:
t2≈0.3265
4. Calculate t:
Taking the square root:
t≈√0.3265≈0.57 seconds
Step 2: Calculate the horizontal distance traveled
1. Identify the horizontal motion:
- Initial horizontal velocity (v) = 1100 m/s (the speed of the bullet)
- Time (t) = 0.57 seconds (calculated from Step 1)
2. Use the formula for horizontal distance:
The horizontal distance (d) can be calculated using:
d=v⋅t
Substituting the known values:
d=1100⋅0.57
3. Calculate d:
d≈627 meters
Final Results
- Time to strike the ground: 0.57 seconds
- Horizontal distance traveled: 627 meters
- Height (h) = 1.6 m (the bullet is fired from this height)
- Initial vertical velocity (u) = 0 m/s (the bullet is fired horizontally)
- Acceleration due to gravity (a) = -9.8 m/s² (downward)
The equation we will use is:
h=ut+12at2
Substituting the known values into the equation:
−1.6=0⋅t+12(−9.8)t2
This simplifies to:
−1.6=−4.9t2
Rearranging gives:
t2=1.64.9
Calculating this:
t2≈0.3265
Taking the square root:
t≈√0.3265≈0.57 seconds
- Initial horizontal velocity (v) = 1100 m/s (the speed of the bullet)
- Time (t) = 0.57 seconds (calculated from Step 1)
The horizontal distance (d) can be calculated using:
d=v⋅t
Substituting the known values:
d=1100⋅0.57
d≈627 meters
- Time to strike the ground: 0.57 seconds
- Horizontal distance traveled: 627 meters
Topper's Solved these Questions
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (MORE THAN ONE CORRECT CHOICE TYPE)
3 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PRACTICE QUESTIONS (LINKED COMPREHENSION)
14 Videos
- MOTION IN TWO AND THREE DIMENSIONSBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION IN TWO AND THREE DIMENSIONSEXERCISE - PROBLEMS
50 Videos
- MOTION ALONG A STRAIGHT LINEBOOK - RESNICK AND HALLIDAYCHAPTER - MOTION ALONG A STRAIGHT LINEEXERCISE - PRACTICE QUESTIONS ( Integer Type )
3 Videos
- OSCILLATIONSBOOK - RESNICK AND HALLIDAYCHAPTER - OSCILLATIONSEXERCISE - Practice Questions
57 Videos
Similar Questions
A ball is thrown horizontally from a point 100m above the ground with a speed of 20m/s. Find (a) the time it takes to reach the ground, (b) the horizontal distance it travels before reaching the ground, (c) the velocity (direction and magnitude) with which it strikes the ground.
View SolutionWhat travels faster : a rifle bullet or the sound of the shot fired from it ?
View Solution
Knowledge Check
A bullet is dropped from the same height when another bullet is fired horizontally. They will hit the ground
AOne after the otherBSimultaneouslyCDepends on the observerDNone of the above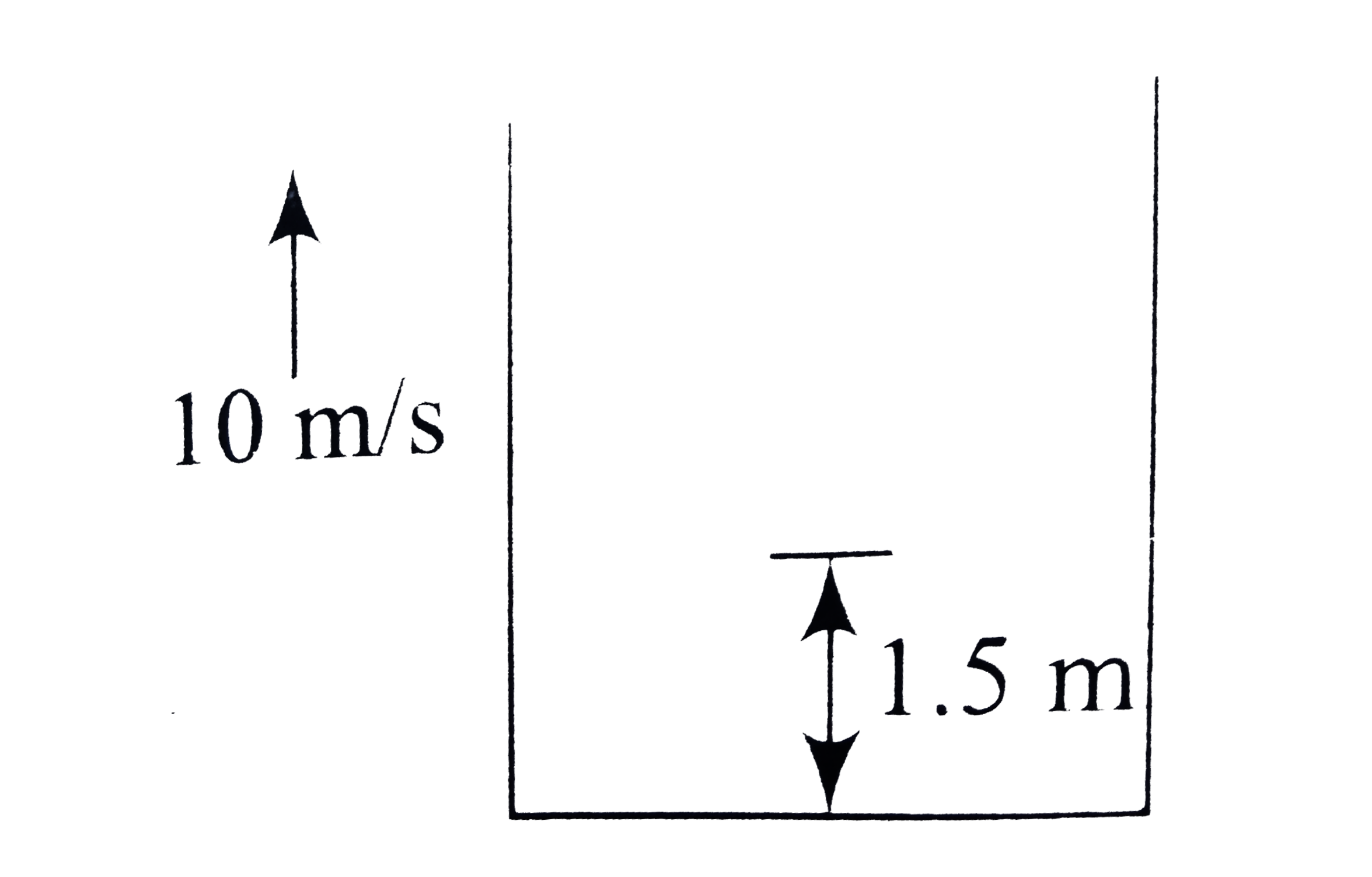
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the distance travelled by bullet during its flight:A32.0mB30.0mC50.0mD35.0mA bullet is fired vertically up from a 400 m tall tower with a speed 80 m/s. If g is taken as 10m/s2, the time taken by the bullet to reach the ground will be
A8 sB16 sC20 sD24 s
A bullet fired from a rifle attains a maximum height of 5 m and crosses a range of 200 m. Find the angle of projection.
View SolutionA bullet of mass 0.01 kg is fired from a gun weighing 5.0 kg. If the initial speed of the bullet is 250 m/s, calculate the speed with which the gun recoils.
View Solution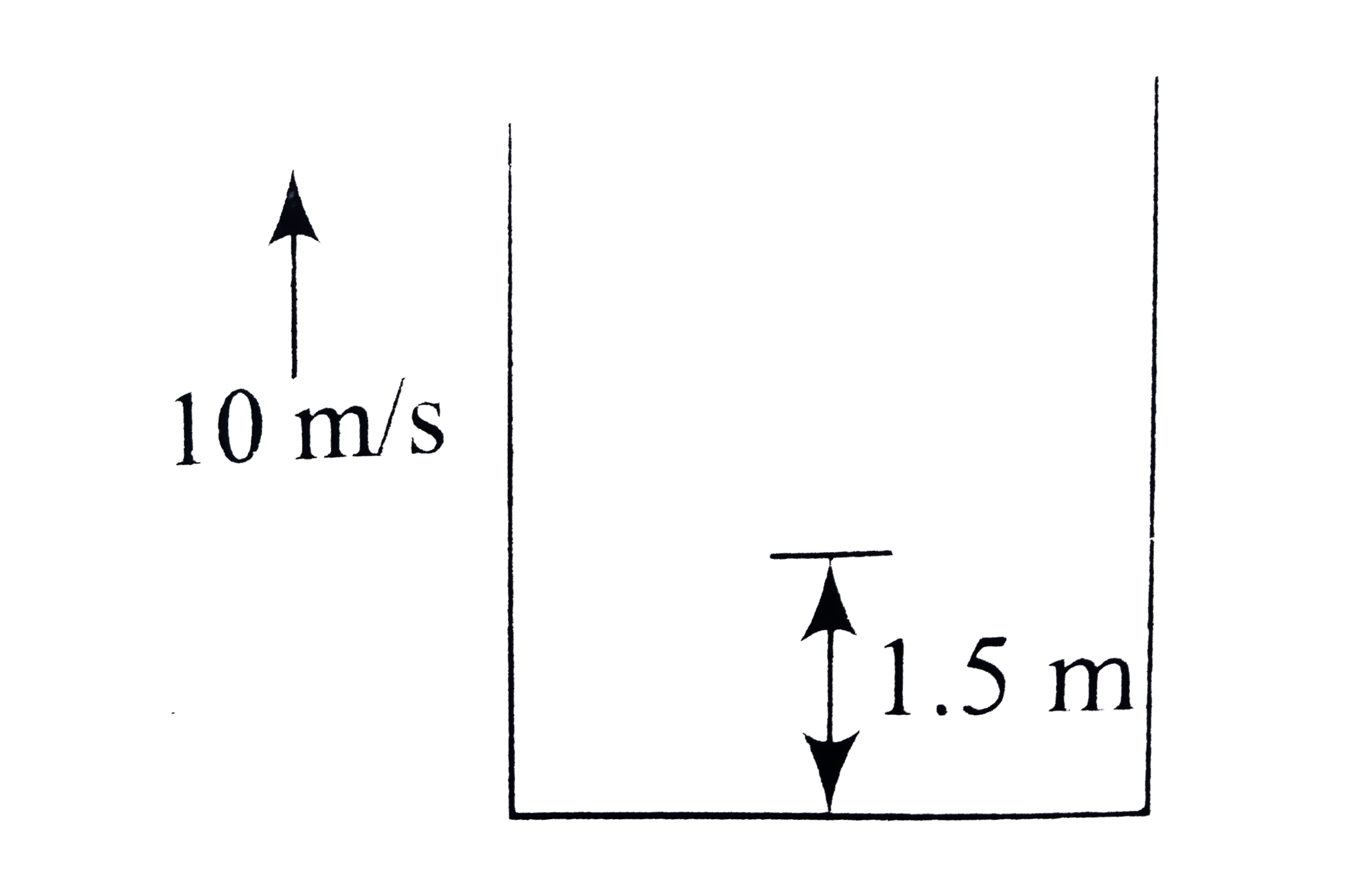
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the maximum height reached by the bullet relative to the ground :
View Solution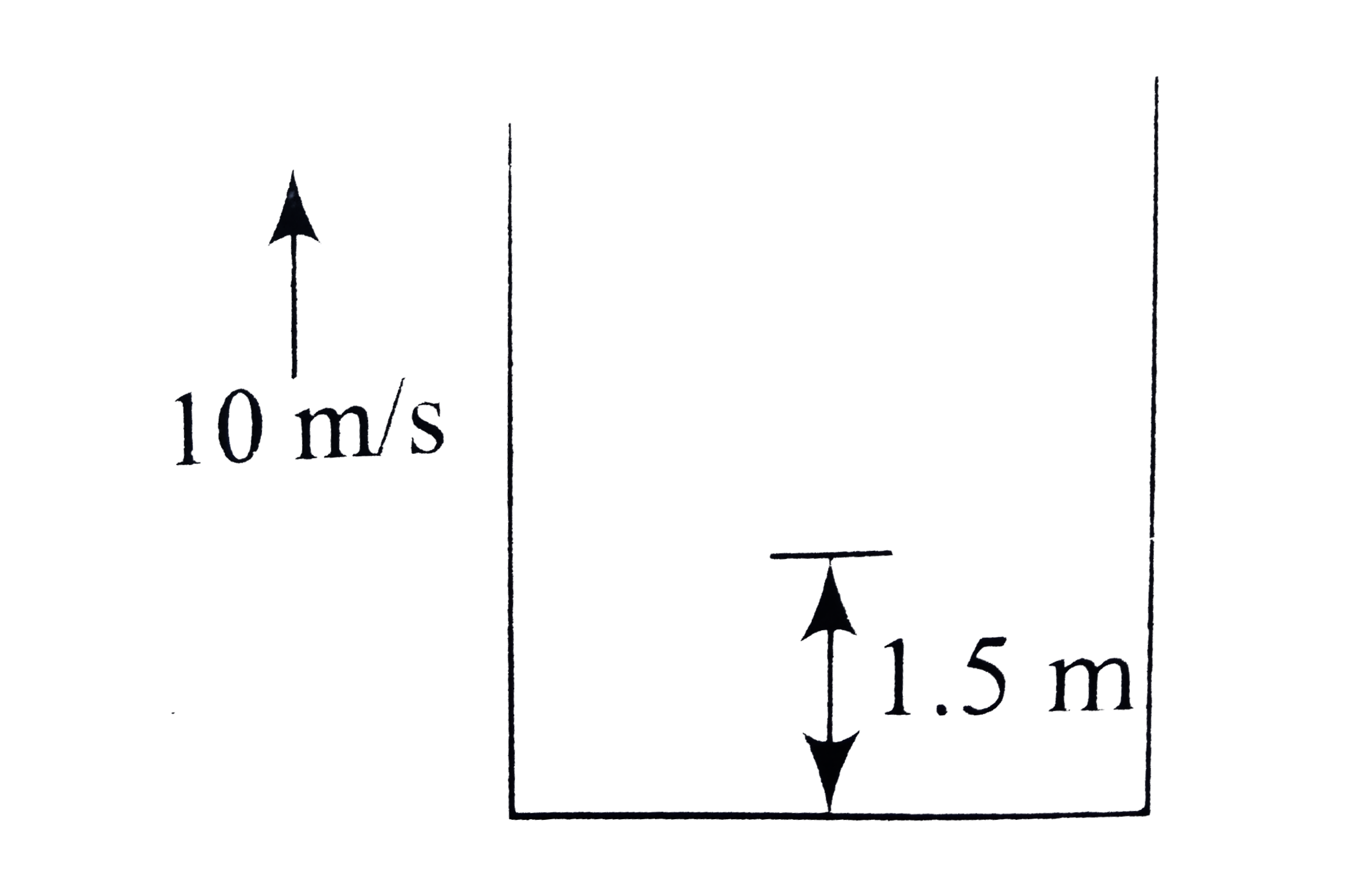
A boy in the elevator shoots a bullet in a vertical upward direction from a height of 1.5 m above the floor of the elevator. There is no roof in the elevator. The floor of the elevator is at 50 m from ground at the instant when velocity of the elevator is 10 m/s in upward direction. The bullet strikes the floor of the elevator in 2 seconds. The initial speed of the bullet is 15 m/s relative to the elevator.
Q. Find the displacement of the bullet relative to ground during its flight:
View SolutionA 10 gm bullet is fired from a rifle horizontally into a 5 kg block of wood suspended by a string and the bullet gets embedded in the block. The impact causes the block to swing to a height of 2.5cm above its initial level. The velocity of the bullet is
View Solution
