Question

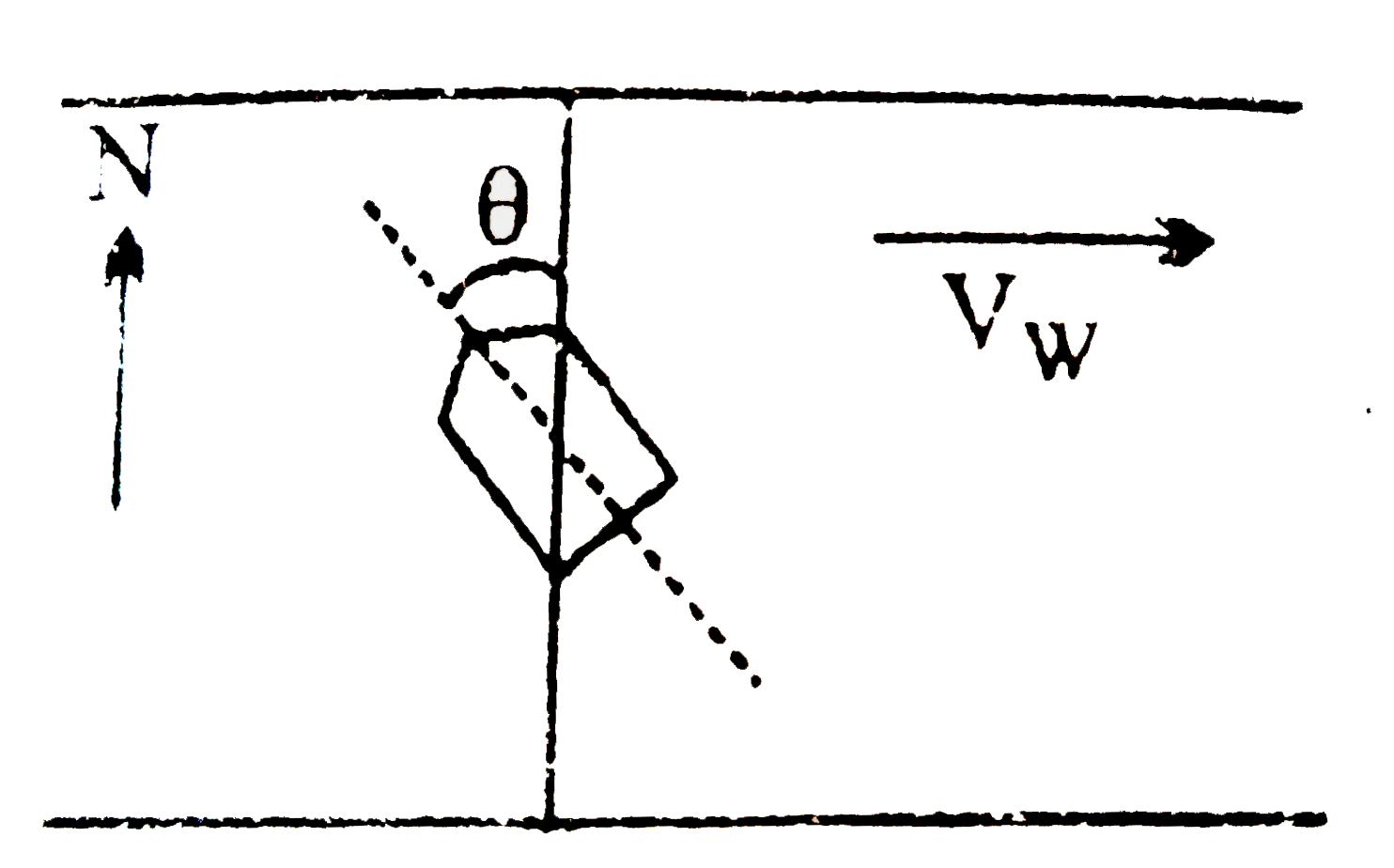
A boat is to go straight across a stream that is flowing at 5.0 km/h to east. The boatman knows that his speed with respect to water is 10 km/h. the angle $\theta$ at which he must head the boat, and his speed relative to the shore will be

Options

A. 10 km/h at `0^(@)`
B. `5sqrt(3) km//s` at `30^(@)`
C. `10sqrt(3) km//h " at" 30^(@)`
D. `5sqrt(3) km//h "at" 60^(@)`

Answer

2

Explanation

Direction of boat velocity is perpendicular to the stream, thus component of the velocity along the river will be zero
`u sin theta=v" " rArr " " sin theta=5//10=1//2`
`rArr " " theta=30^(@)`
& velocity relative to shore=`10cos 30 ^(@)=5sqrt(3)`