Two particles of equal mass 'm' are projected from the ground with speed v1 and v2 at angles θ1 and θ2 at the same times as shown in figure. The centre of mass of the two particles.

will move in a vertical line if v1tanθ=v2tanθ2
will move in a vertical line if v1sinθ=v2sinθ2
will move In a vertical line if v1cotθ1=v2cotθ2
will move in a vertical line if v1cosθ1=v2cosθ2
The correct Answer is:4
Xcm(t)=vcosθ1t−v2cosθ2t2
Ycm(t)=(v1sinθ1−gt)+(v2sinθ2−gt)2
Xcm=0 when v1cosθ1=v2cosθ
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A particle of mass m is projected at t=0 from the point P on the ground with speed v0 at an angle of θ to the horizontal. Find the magnitude and direction of the angular momentum of the particle at time t=v0sinθ2g.
View SolutionIf two particles of masses m1 and m2 are projected vertically upwards with speed v1 and v2, then the acceleration of the centre of mass of the system is
View Solution
Knowledge Check
Two particles of equal mass in are projected from the ground with speeds v1 and v2 at angles θ1, and θ2 as shown in the figure. Given θ2>θ1 and v1cosθ1=v2cosθ2Which statement/s is/are correct?
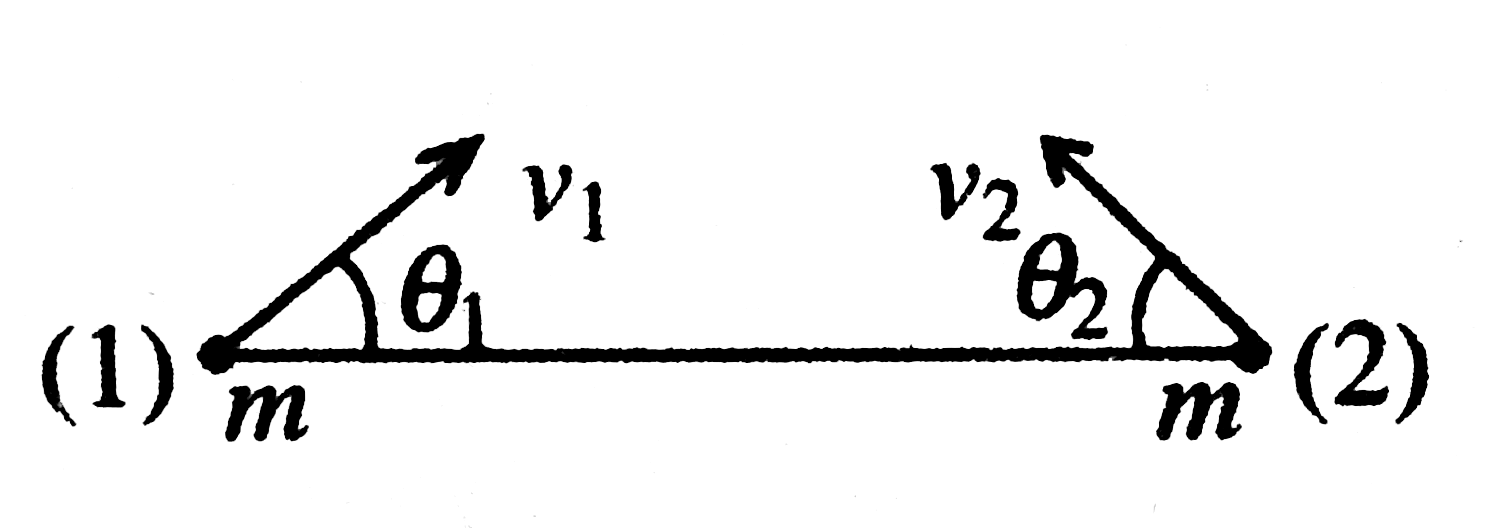 ACentre of mass of particles will move along a vertical line.BCentre of mass of particles will move along a line inclined at some angle with vertical.CParticle '1' will be above vertical. centre of mass level when both particles are in air.DParticle '2' will be above centre of mass level both particles are in air.
ACentre of mass of particles will move along a vertical line.BCentre of mass of particles will move along a line inclined at some angle with vertical.CParticle '1' will be above vertical. centre of mass level when both particles are in air.DParticle '2' will be above centre of mass level both particles are in air.Trajectory of two particles projected from origin with speeds v1 and v2 at angles θ1 and θ2 with positive x- axis respectively are as shown in the figure. Given that (g=−10m/s2(ˆj)). Choose the correct option related to diagram.
 Av1−v2=2v1Bθ2−θ1=2θ1C3(v1−v2)=v1D3(θ2−θ1)=θ1
Av1−v2=2v1Bθ2−θ1=2θ1C3(v1−v2)=v1D3(θ2−θ1)=θ1Two particles are projected at the same instant with speeds v1 and v2 making angles α and β with the horizontal as shown in the figure. Nelecting air resistance, the trajectory of the mass center the two particles
 Acan be a vertical straight lineBcan be a horizontal straight lineCis a straight lineDis a parabola
Acan be a vertical straight lineBcan be a horizontal straight lineCis a straight lineDis a parabola
A particle is projected at an angle θ from ground with speed u (g = 10 m/s2 )
View SolutionTwo particles are projected in air with speed v0 at angles θ1 and θ2 (both acute) to the horizontal,respectively.If the height reached by the first particle greater than that of the second,then thick the right choices
View SolutionTwo projectiles are thrown simultaneously in the same plane from the same point. If their velocities are v1 and v2 at angles θ1 and θ2 respectively from the horizontal, then ansewer the following questions
The trajectory of particle 1 with respect to particle 2 wil be
View SolutionTwo particles are projected from the same point with the same speed at different angles θ1 & θ2 to the horizontal. They have the same range. Their times of flight are t1 & t2 respectily
View SolutionTwo particles are projected from the same point with the same speed at different angles θ1 and θ2 to the horizontal. If their respective times of flights are T1 and T2 and horizontal ranges are same then
a) θ1+θ2=90∘ ,
b)T1=T2tanθ1
c.T1=T2tanθ2 ,
d) T1sinθ2=T2sinθ1
View Solution
