A particle of mass $m$ is projected at $t = 0$ from the point $P$ on the ground with speed $v_{0}$ at an angle of $θ$ to the horizontal. Find the magnitude and direction of the angular momentum of the particle at time $t = \frac{v_{0} sin θ}{2 g}$ .

Video Solution

Text Solution

Verified by Experts

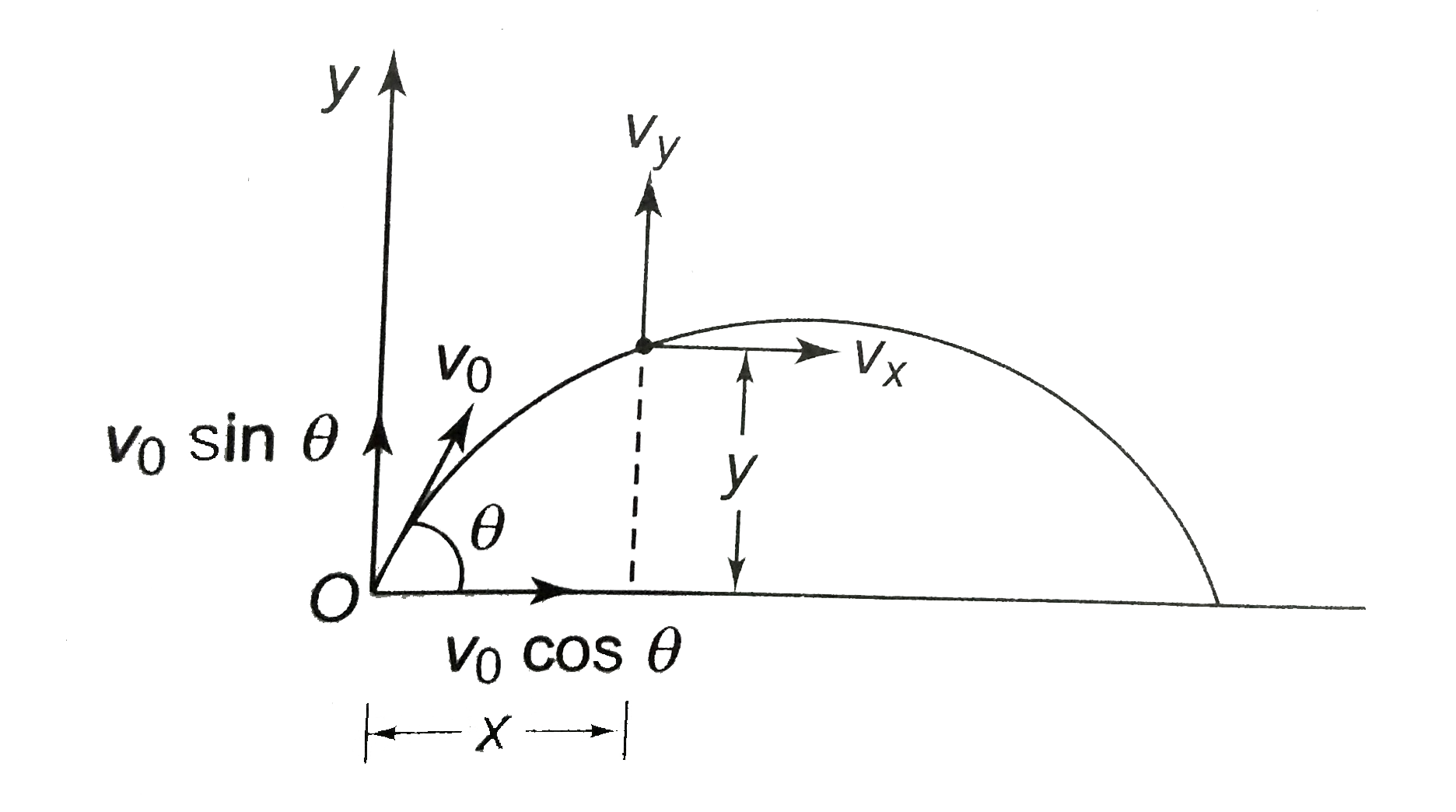
$t = \frac{v_{0} sin θ}{2 g}$
$x : v_{x} = v_{0} cos θ$
$x = v_{0} cos θ t = v_{0} cos θ \times \frac{v_{0} sin θ}{2 g} = \frac{v_{0}^{2} sin θ cos θ}{2 g}$
$y : v_{y} = v_{0} sin θ - gt$
$= v_{0} sin θ - g \times \frac{v_{0} sin θ}{2 g} = \frac{v_{0} sin θ}{2}$
$y = v_{0} sin θ t - \frac{1}{2} {gt}^{2}$
$= v_{0} sin θ \times \frac{v_{0} sin θ}{2 g} - \frac{1}{2} {g (\frac{v_{0} sin θ}{2 g})}^{2}$
$= \frac{v_{0}^{2} {sin}^{2} θ}{2 g} - \frac{v_{0}^{2} {sin}^{2} θ}{8 g} = \frac{3}{8} \frac{v_{0}^{2} {sin}^{2} θ}{g}$
$L = m v_{x} y - m v_{y} x$
$= m (v_{0} cos θ \times \frac{3}{8} \frac{v_{0}^{2} {sin}^{2} θ}{g} - \frac{v_{0} sin θ}{2} \times \frac{v_{0}^{2} sin θ cos θ}{2 g})$
$= \frac{n v_{0}^{3} {sin}^{2} θ cos θ}{8 g}$
OR
In vector form
$\to v = v_{x} ˆ i + v_{y} ˆ j, \to r = x ˆ i + y ˆ j$
$\to L = \to r \times \to p = \to r \times m \to v = m ∣ ∣ ∣ ∣ ∣ \begin{matrix} i & j & k x & y & o v_{x} & v_{y} & o \end{matrix} ∣ ∣ ∣ ∣ ∣$
$= m (x y_{y - y v_{x}}) ˆ k$
$= m [\frac{v_{0}^{2} sin θ cos θ}{2} \times \frac{v_{0} sin θ}{2} - \frac{3}{8} \times \frac{v_{0}^{2} {sin}^{2} θ}{g} \times v_{0} cos θ] ˆ k$
$m = [- \frac{1}{8} \frac{v_{0}^{3} {sin}^{2} θ cos θ}{g}] {ˆ k}^{~}$
$\to L = \frac{- m v_{0}^{3} {sin}^{2} θ cos θ}{8 g} ˆ k$
$L = ∣ ∣ \to L ∣ ∣ = \frac{m v_{0}^{3} {sin}^{2} θ cos θ}{8 g}$

Updated on:21/07/2023