A skier plane to ski a smooth fixed hemisphere of radius . He starts from rest from top of a curve smooth surface of height . The angle at which he leaves the hemisphere is 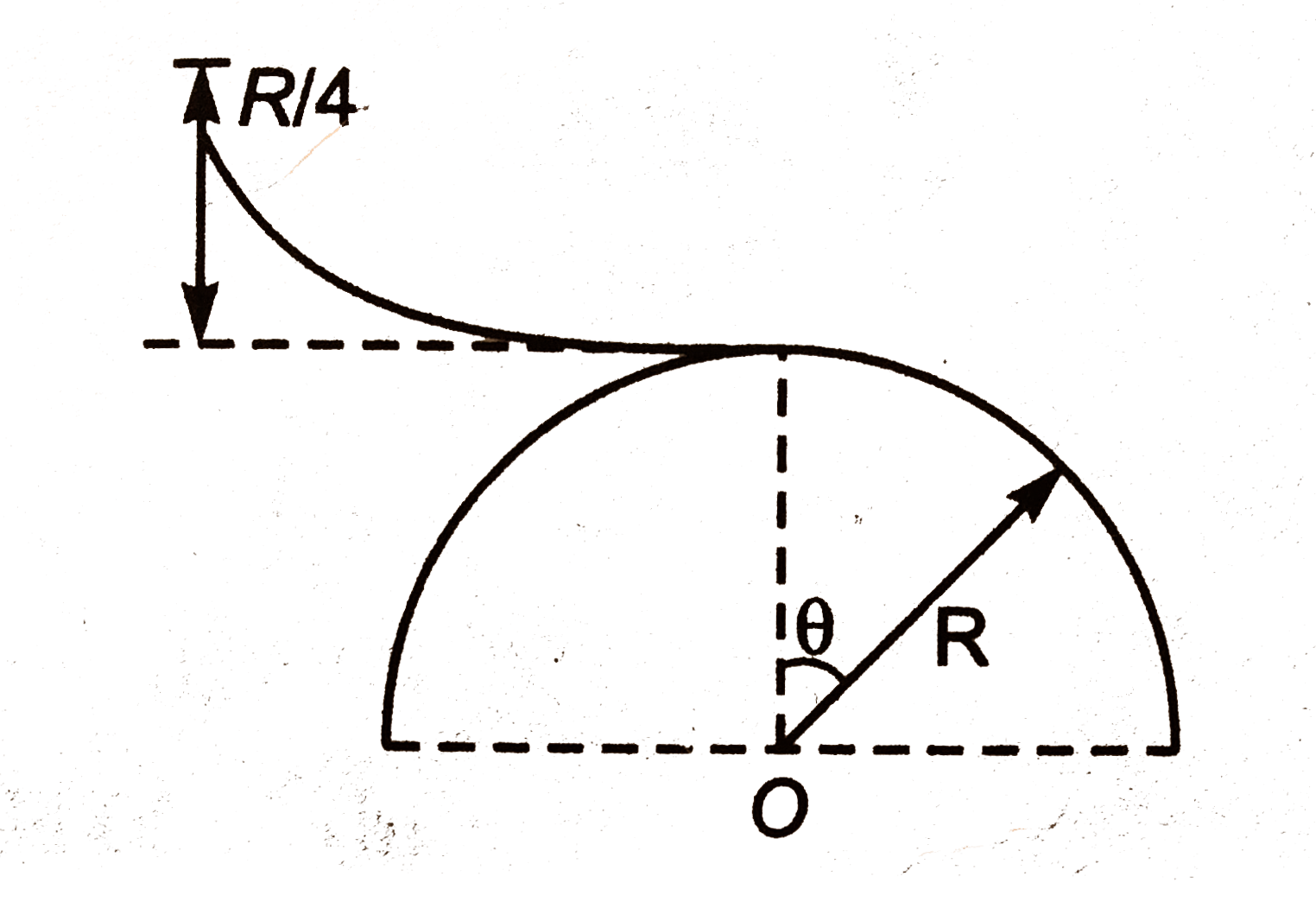
The correct Answer is:3
Conservation energy between points A and B
Also EFD at point B will be give

Topper's Solved these Questions
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (A)
Explore 32 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (B)
Explore 3 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART- C
Explore 4 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
A particle of mass m is placed in equlibrium at the top of a fixed rough hemisphere of radius R. Now the particle leaves the contact with the surface of the hemisphere at angular position θ with the vertical wheere cosθ35. if the work done against frictiion is 2mgR10x, find x.
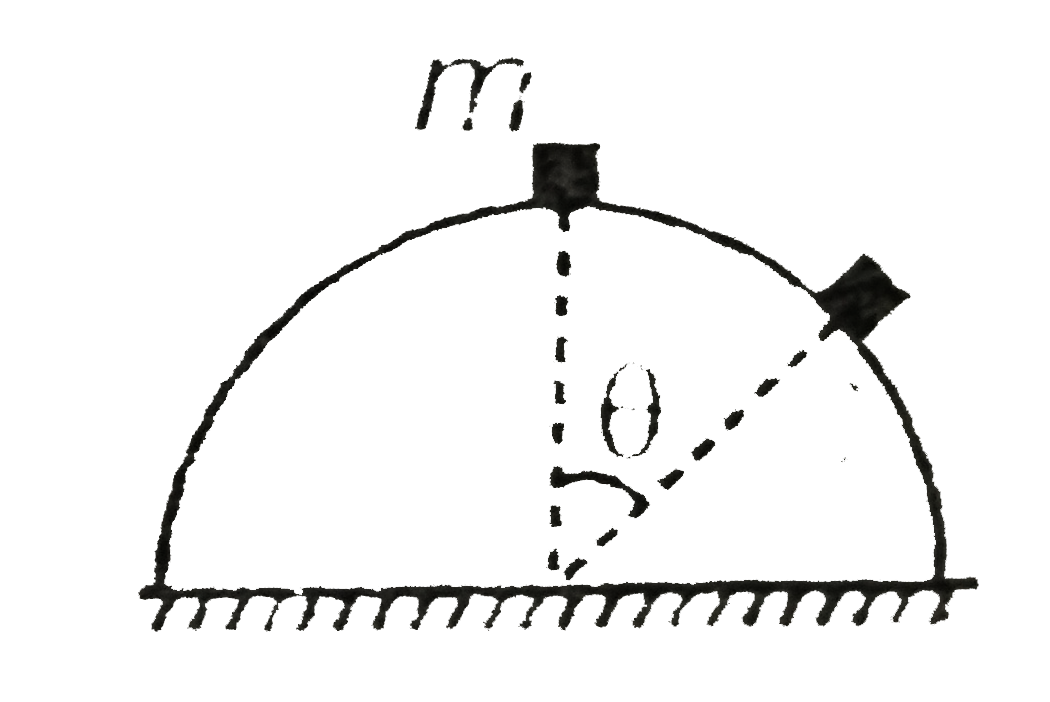
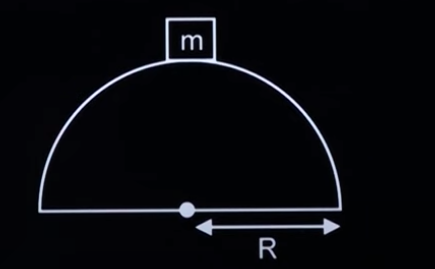
View SolutionA block of mass as shown is released from rest from top of a fixed smooth hemisphere. Find angle made by this particle with vertical at the instant when it looses contact with hemisphere.
View Solution
Knowledge Check
A skier plane to ski a smooth fixed hemisphere of radius R . He starts from rest from a curve smooth surface of height (R4) . The angle θ at which he leaves the hemisphere is
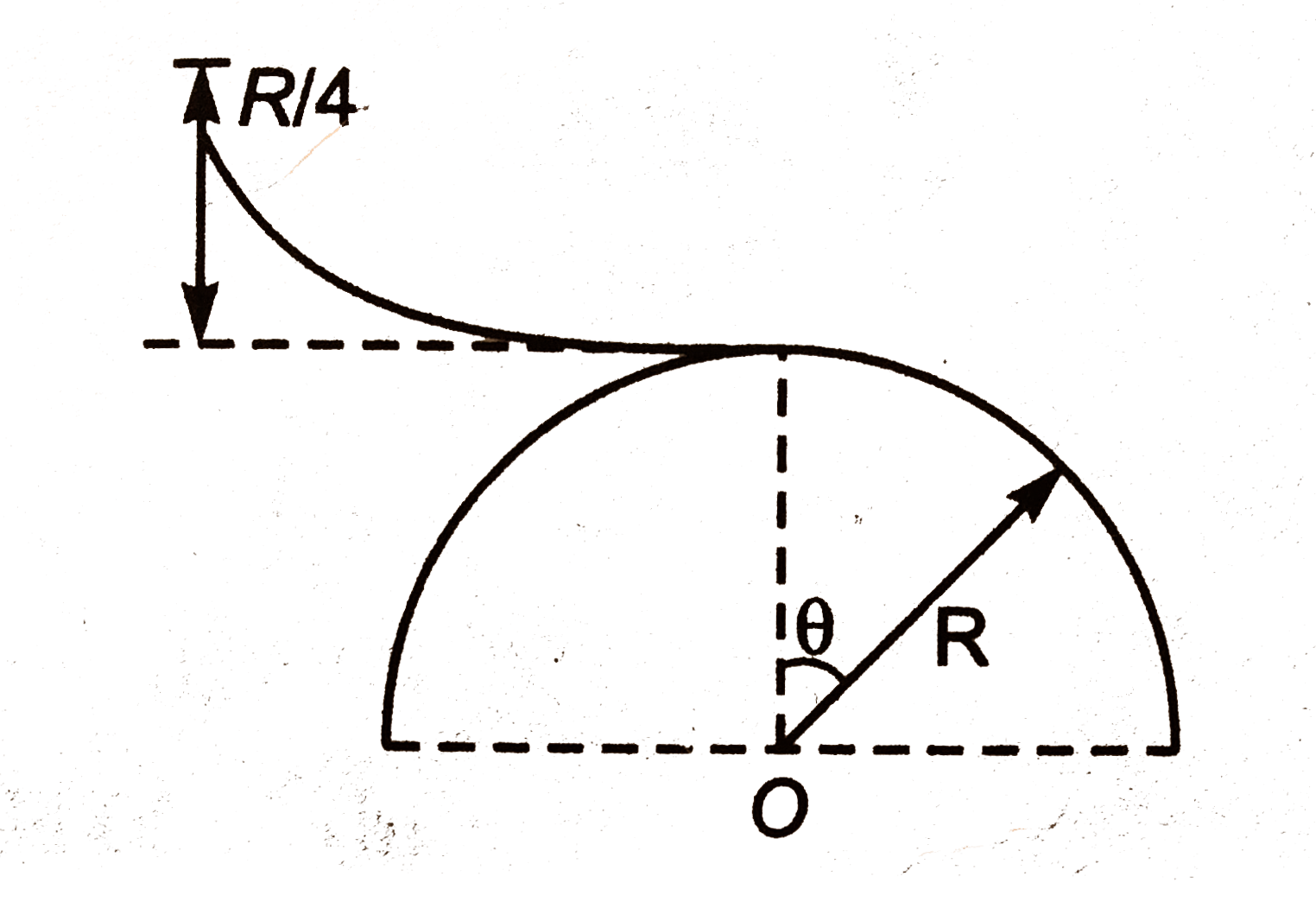 Acos−1(23)Bcos−1(5)√3Ccos−1(56)Dcos−1[52√3]
Acos−1(23)Bcos−1(5)√3Ccos−1(56)Dcos−1[52√3]A skier plans to ski a smooth fixed hemisphere of radius R He starts from rest from a curved smooth surface of height (R/4) the angle θ at which he leaves the hemisphere is
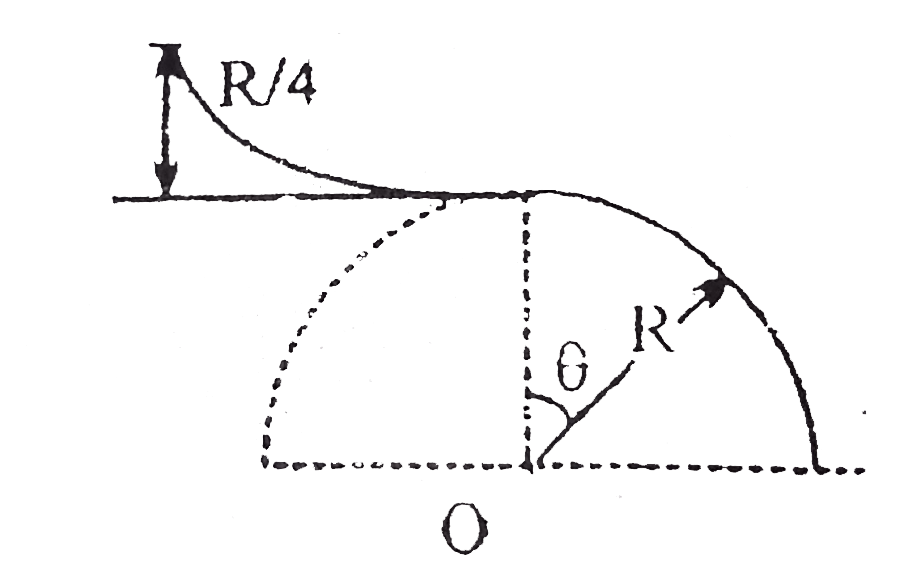 Acos−1(2/3)Bcos−1(5/√3Ccos−1(5/6)Dcos−1(5/2√3
Acos−1(2/3)Bcos−1(5/√3Ccos−1(5/6)Dcos−1(5/2√3A ball of mass m and radius r rolls inside a fixed hemispherical shell of radius R. It is released from rest from point A as shown in figure. The angular velocity of centre of the ball in position B about the centre of the shell is.
 .A2√g5(R−r)B√10g7(R−r)C√g7(R−r)D√5g2(R−r)
.A2√g5(R−r)B√10g7(R−r)C√g7(R−r)D√5g2(R−r)
Find the CG of :(a) a cone of height h from the base,(b) a hemisphere of radius r from its flat surface.
View SolutionAn object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
View SolutionA small block of mass m projected horizontally from the top of the smooth and fixed hemisphere of radius r with speed u as shown. For values of u≥u0(u0=√gr) it does not slide on the hemisphere. l i.e., leaves the surface at the top itself.

For u=u0/3, Find the height from the ground at which it leaves the hemisphere
View SolutionA body of mass Mkg is on the top point of a smooth hemisphere of radius 5m . It is released to slide down the surface of hemisphere it leaves the surface when its velocity is 5ms−1 At this instant the angle made by the radius vector of the body with the vertical is ( Take g=10m/s2)
View SolutionA small block of mass m projected horizontally from the top of the smooth and fixed hemisphere of radius r with speed u as shown. For values of u≥u0(u0=√gr) it does not slide on the hemisphere. l i.e., leaves the surface at the top itself.
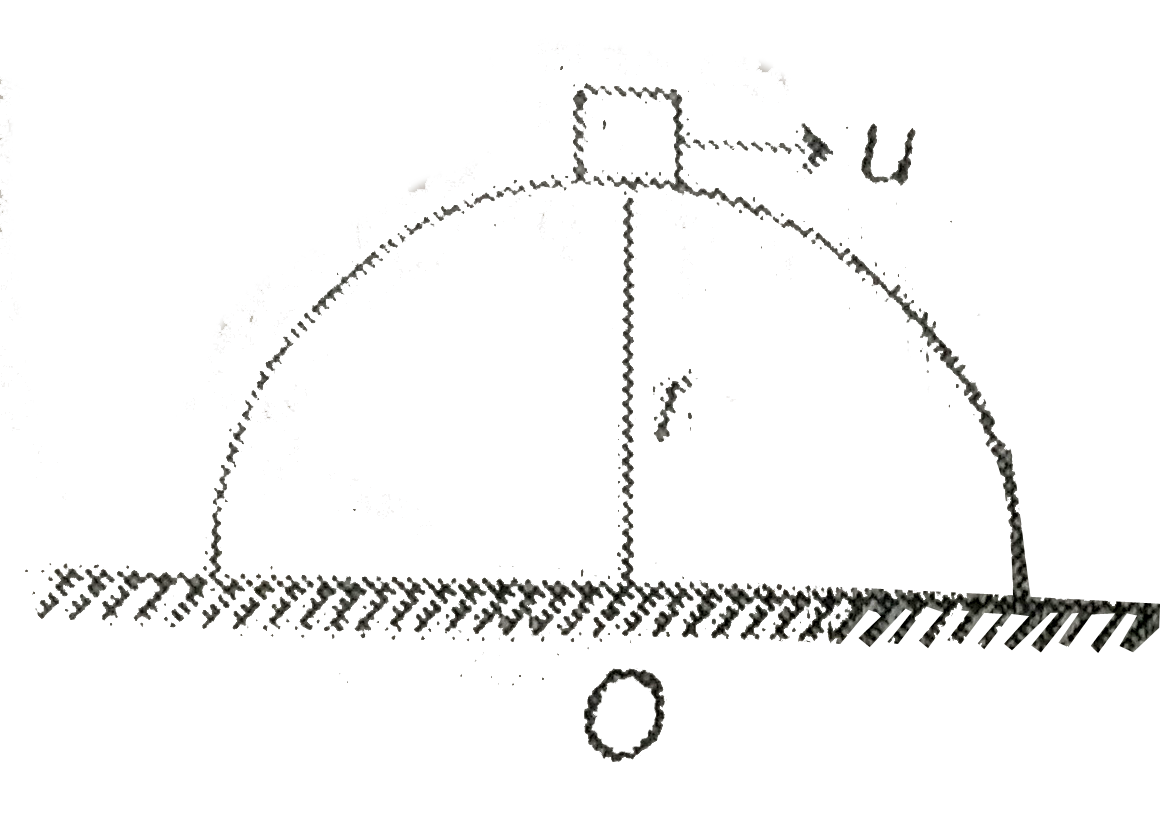
In the above problem find its net acceleration at the instant it levels the hemisphere.
View Solution