What can be said about velocity of the object if its displacement-time graph is parallel to displacement axis?
To determine what can be said about the velocity of an object when its displacement-time graph is parallel to the displacement axis, we can follow these steps:
1. Understanding the Graph:
- A displacement-time graph shows how displacement changes over time. If the graph is parallel to the displacement axis (y-axis), it indicates that the displacement remains constant over time.
2. Definition of Velocity:
- Velocity is defined as the rate of change of displacement with respect to time. Mathematically, this is expressed as:
v=dsdt
where v is velocity, ds is the change in displacement, and dt is the change in time.
3. Analyzing the Slope:
- The slope of the displacement-time graph represents the velocity of the object. If the graph is parallel to the displacement axis, it means there is no change in displacement as time progresses.
4. Slope Calculation:
- In a graph where the line is parallel to the displacement axis, the angle θ between the line and the time axis (x-axis) is 90 degrees. The slope can be expressed as:
slope=tan(θ)
- Since θ=90∘, we have:
tan(90∘)=∞
This indicates that the slope is infinite.
5. Conclusion about Velocity:
- Since the slope of the displacement-time graph is infinite, it implies that the velocity of the object is also infinite. Thus, we conclude that if the displacement-time graph is parallel to the displacement axis, the velocity of the object is infinite.
Final Answer:
If the displacement-time graph is parallel to the displacement axis, the velocity of the object is infinite.
---
- A displacement-time graph shows how displacement changes over time. If the graph is parallel to the displacement axis (y-axis), it indicates that the displacement remains constant over time.
- Velocity is defined as the rate of change of displacement with respect to time. Mathematically, this is expressed as:
v=dsdt
where v is velocity, ds is the change in displacement, and dt is the change in time.
- The slope of the displacement-time graph represents the velocity of the object. If the graph is parallel to the displacement axis, it means there is no change in displacement as time progresses.
- In a graph where the line is parallel to the displacement axis, the angle θ between the line and the time axis (x-axis) is 90 degrees. The slope can be expressed as:
slope=tan(θ)
- Since θ=90∘, we have:
tan(90∘)=∞
This indicates that the slope is infinite.
- Since the slope of the displacement-time graph is infinite, it implies that the velocity of the object is also infinite. Thus, we conclude that if the displacement-time graph is parallel to the displacement axis, the velocity of the object is infinite.
If the displacement-time graph is parallel to the displacement axis, the velocity of the object is infinite.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:REVISION EXERCISE (FILL IN THE BLANKS)
Explore 10 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:REVISION EXERCISE (SHORT ANSWER QUESTIONS)
Explore 19 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:HIGHER ORDER THINKING SKILL AND ADVANCED LEVEL QUESTION WITH ANSWER
Explore 5 Videos
- MOTION IN A PLANE Book:MODERN PUBLICATIONChapter:MOTION IN A PLANE Exercise:Chapter Practice Test
Explore 15 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Practice Test (For Board Examination)
Explore 12 Videos
Similar Questions
What does the slope of displacement-time graph give?
View SolutionWhat can you say about the motion of a body if
(a) its displacement-time graph is a straight line, with some slope.
(b) its velocity-time graph is a straight line, with some slope ?
View SolutionThe average velocity of a particles is equal to its displacement-time graph ?
View SolutionGraphs(Displacement-time)
View SolutionWhat can you say about the motion of a body if :
(a) its displacement-time graph is a straight line ?
(b) its velocity-time graph is a straight line ?
View SolutionWhat can you say about the motion of a body if its speed-time graph is a straight line parallel to the time axis ?
View SolutionThe velocity of particle (whose displacement time graph is shown) at t=3
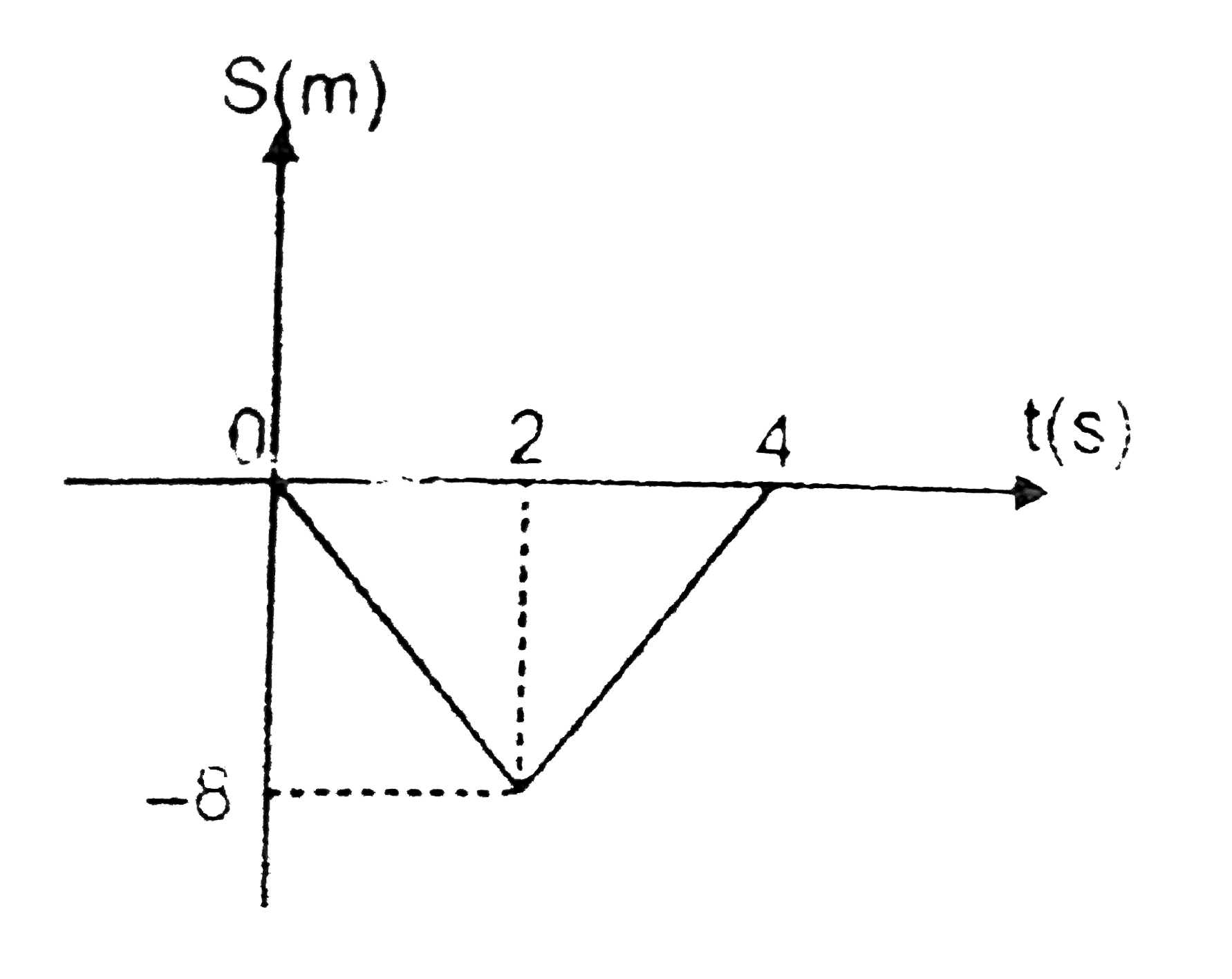 .
.
View SolutionWhat can you say about the motion of an object whose distance-time graph is a straight line parallel to the time axis ?
View SolutionAn object is thrown upward with a velocity u, then displacement -time graph is
View SolutionWhat can you say about the motion of an object whose distance-time graph is a straight line parallel to the time axis ?
View Solution

