A body is falling freely under gravity. It passes two points A and B (A being higher than B) 20m apart vertically in 2s. Find the elevation of the point above A from where it began to fall.
To solve the problem step by step, we can follow these steps:
Step 1: Understand the Problem
We have a body falling freely under gravity. It passes two points A and B, which are 20 meters apart vertically, in a time of 2 seconds. We need to find the height (H1) above point A from which the body was released.
Step 2: Define Variables
- Let H1 be the height from which the body is released to point A.
- Let H2 be the height from which the body is released to point B.
- The distance between points A and B is given as H2−H1=20 m.
- The time taken to travel from A to B is 2 seconds.
Step 3: Use the Equations of Motion
Since the body is falling freely under gravity, we can use the second equation of motion:
s=ut+12at2
Where:
- s is the distance traveled,
- u is the initial velocity (which is 0 since it starts from rest),
- a is the acceleration due to gravity (approximately 9.8m/s2),
- t is the time.
Step 4: Calculate H1
For the distance H1 (from the point of release to point A):
H1=0⋅t+12gt2=12gt2
Where t is the time taken to reach point A.
Step 5: Calculate H2
For the distance H2 (from the point of release to point B):
H2=0⋅(t+2)+12g(t+2)2=12g(t+2)2
Step 6: Set Up the Equation
From the previous steps, we have:
H2−H1=20
Substituting the expressions for H1 and H2:
12g(t+2)2−12gt2=20
Factoring out 12g:
12g((t+2)2−t2)=20
Step 7: Simplify the Equation
Expanding (t+2)2:
(t+2)2−t2=t2+4t+4−t2=4t+4
Thus, we have:
12g(4t+4)=20
g(4t+4)=40
4t+4=40g
Substituting g≈9.8m/s2:
4t+4=409.8
Calculating:
4t+4≈4.08
4t≈4.08−4
4t≈0.08⟹t≈0.02s
Step 8: Calculate H1
Now substituting t back into the equation for H1:
H1=12gt2=12⋅9.8⋅(0.02)2
Calculating:
H1=12⋅9.8⋅0.0004≈0.00196m≈0.002m
Final Answer
The elevation of the point above A from where it began to fall is approximately 0.002 meters.
---
We have a body falling freely under gravity. It passes two points A and B, which are 20 meters apart vertically, in a time of 2 seconds. We need to find the height (H1) above point A from which the body was released.
- Let H1 be the height from which the body is released to point A.
- Let H2 be the height from which the body is released to point B.
- The distance between points A and B is given as H2−H1=20 m.
- The time taken to travel from A to B is 2 seconds.
Since the body is falling freely under gravity, we can use the second equation of motion:
s=ut+12at2
Where:
- s is the distance traveled,
- u is the initial velocity (which is 0 since it starts from rest),
- a is the acceleration due to gravity (approximately 9.8m/s2),
- t is the time.
For the distance H1 (from the point of release to point A):
H1=0⋅t+12gt2=12gt2
Where t is the time taken to reach point A.
For the distance H2 (from the point of release to point B):
H2=0⋅(t+2)+12g(t+2)2=12g(t+2)2
From the previous steps, we have:
H2−H1=20
Substituting the expressions for H1 and H2:
12g(t+2)2−12gt2=20
Factoring out 12g:
12g((t+2)2−t2)=20
Expanding (t+2)2:
(t+2)2−t2=t2+4t+4−t2=4t+4
Thus, we have:
12g(4t+4)=20
g(4t+4)=40
4t+4=40g
Substituting g≈9.8m/s2:
4t+4=409.8
Calculating:
4t+4≈4.08
4t≈4.08−4
4t≈0.08⟹t≈0.02s
Now substituting t back into the equation for H1:
H1=12gt2=12⋅9.8⋅(0.02)2
Calculating:
H1=12⋅9.8⋅0.0004≈0.00196m≈0.002m
The elevation of the point above A from where it began to fall is approximately 0.002 meters.
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:PRACTICE PROBLEMS
Explore 28 Videos
- MOTION IN A STRAIGHT LINE Book:MODERN PUBLICATIONChapter:MOTION IN A STRAIGHT LINE Exercise:CONCEPTUAL QUESTIONS
Explore 14 Videos
- MOTION IN A PLANE Book:MODERN PUBLICATIONChapter:MOTION IN A PLANE Exercise:Chapter Practice Test
Explore 15 Videos
- OSCILLATIONS Book:MODERN PUBLICATIONChapter:OSCILLATIONS Exercise:Practice Test (For Board Examination)
Explore 12 Videos
Similar Questions
A body falling freely under gravity passes two points 30 m apart in 1 s. find from what point above the upper point it began to fall ? Take g 9.8−2
View SolutionA cuboidal elevator cabon is shown in the figure. A ball is thrown from point A on the floor of cabon when the elevator is falling under gravity. The plane of motions is ABCD and the angle of projection of the ball with AB, relative to elevator, if the ball collides with point C, is α. Then find the value of tanα.
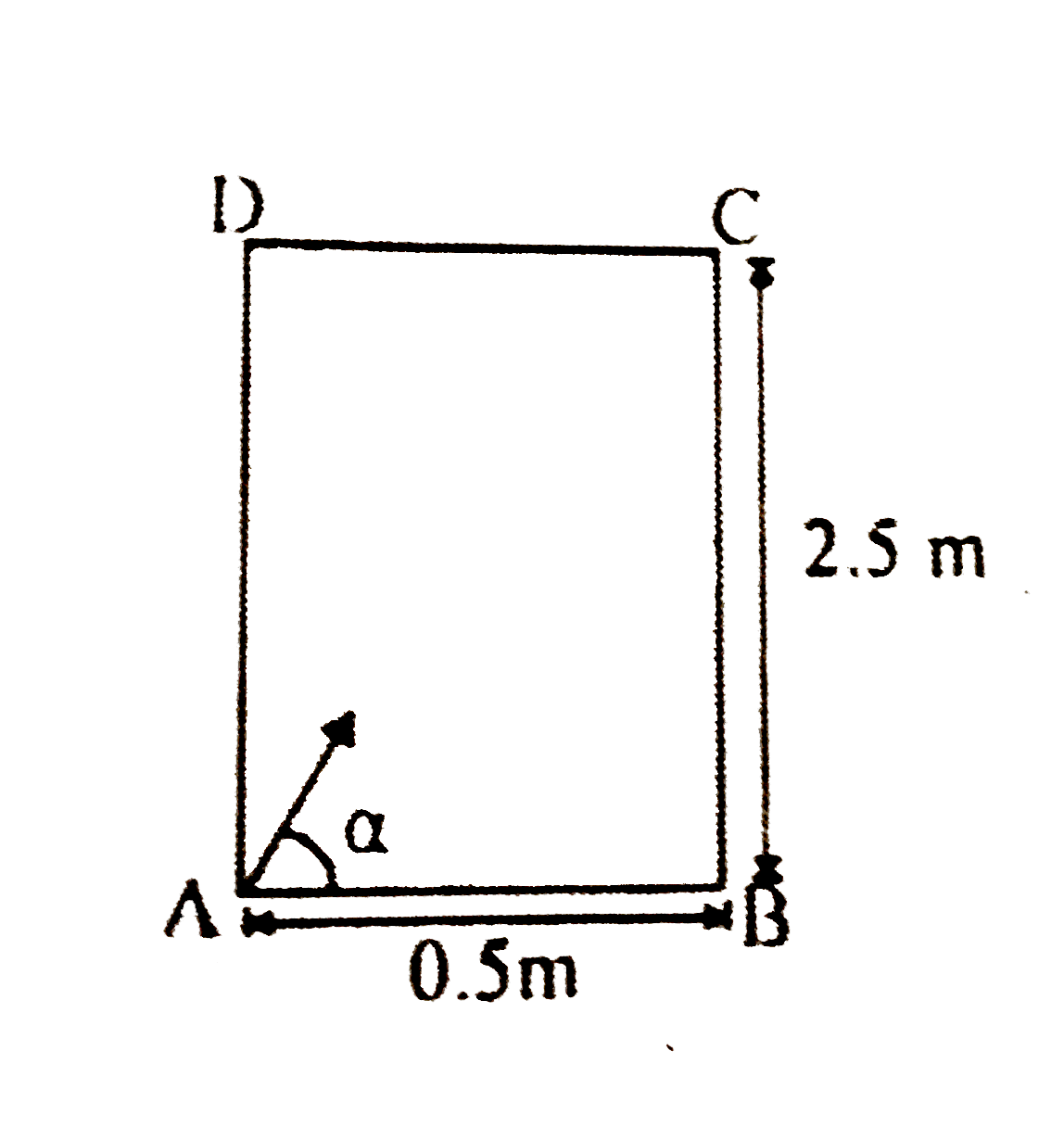
View Solution
Knowledge Check
A body falling freely under the action of gravity passes 2 points 9 m apart vertically in 0.2 s. From what height above the higher point did it start to fall?
A99 mB200 mC20 mD109 mA body falling freely under gravity passes two points 30 m apart in 1 s. From what point above the upper point it began to fall? (Take g = 9.8ms−2).
A32.1 mB16.0 mC8.6 mD4.0 mDuring vertical motion under gravity a body passes through a point at 4s and 12 s in upwards and downwards journeys. The speed at this point is
AgB2gC3gD4g
During vertical motion under gravity a body passes through a point at 4s and 12 s in upwards and downwards journeys. The speed at this point is
View SolutionA body travelling with uniform acceleration crosses two point A and B with velocities 20ms−1 and 30ms−1 respectively. The speed of the body at the mid-point of A and B is.
View SolutionA balloon moving in a straight line passes vertically above two points A and B on a horizontal plane 10ft apart. When above A the balloon has an angle of elevation of 60∘ as seen from B. When above B it has an angle of elevation of 45∘ as seen from A. The distance of B from the point C where it will touch the plane is
View SolutionThe angle of elevation of the loop of a vertical tower standing on a horizontal plane is observed to be 45∘ from a point A on the plane. Let B be the point 30m vertically above the point A. If the angle of elevation of the top of the tower from B be 30∘, then the distance (in m) of the foot of the lower from the point A is:
View SolutionA particle is dropped from point A at a certain height from ground. It falls freely and passes through thre points B,C and D with BC=CD. The time taken by the particle to move from B to CD is 2s and from C to D is 1s. The time taken to move from A to B is s
View Solution

