During vertical motion under gravity a body passes through a point at 4s and 12 s in upwards and downwards journeys. The speed at this point is
g
2g
3g
4g
The correct Answer is:D
To solve the problem of finding the speed of a body at a specific point during its vertical motion under gravity, we can follow these steps:
1. Understanding the Motion:
The body is projected upwards and then comes back down. It passes through a point (let's call it point C) at two different times: 4 seconds on the way up and 12 seconds on the way down.
2. Time Intervals:
The time taken to reach point C on the way up is 4 seconds. The time taken to reach point C on the way down is 12 seconds. The total time taken from the start to the point of maximum height (point B) and back down to point C is 12 seconds.
3. Calculating the Time for Descent:
The time taken to go from point C to point B (maximum height) and then back down to point C is:
Total time from C to B and B to C'=12 seconds−4 seconds=8 seconds
This means the time taken to go from point C to point B (upwards) and back down to point C (downwards) is 8 seconds.
4. Dividing the Time:
Since the motion is symmetrical, the time taken to go from point C to point B (upwards) is equal to the time taken to go from point B back down to point C (downwards). Therefore, each segment (C to B and B to C) takes:
8 seconds2=4 seconds
5. Using the Equation of Motion:
We can use the equation of motion to find the speed at point C when the body is descending:
V=U+at
Here, U (initial velocity at point B) is 0 (since it is at maximum height), a is the acceleration due to gravity g, and t is the time taken to fall from point B to point C, which we found to be 4 seconds.
6. Substituting Values:
Substituting the values into the equation:
V=0+g⋅4=4g
7. Final Answer:
Therefore, the speed of the body at point C is:
V=4g
Conclusion:
The speed at point C, where the body passes at 4 seconds on the way up and 12 seconds on the way down, is 4g.
The body is projected upwards and then comes back down. It passes through a point (let's call it point C) at two different times: 4 seconds on the way up and 12 seconds on the way down.
The time taken to reach point C on the way up is 4 seconds. The time taken to reach point C on the way down is 12 seconds. The total time taken from the start to the point of maximum height (point B) and back down to point C is 12 seconds.
The time taken to go from point C to point B (maximum height) and then back down to point C is:
Total time from C to B and B to C'=12 seconds−4 seconds=8 seconds
This means the time taken to go from point C to point B (upwards) and back down to point C (downwards) is 8 seconds.
Since the motion is symmetrical, the time taken to go from point C to point B (upwards) is equal to the time taken to go from point B back down to point C (downwards). Therefore, each segment (C to B and B to C) takes:
8 seconds2=4 seconds
We can use the equation of motion to find the speed at point C when the body is descending:
V=U+at
Here, U (initial velocity at point B) is 0 (since it is at maximum height), a is the acceleration due to gravity g, and t is the time taken to fall from point B to point C, which we found to be 4 seconds.
Substituting the values into the equation:
V=0+g⋅4=4g
Therefore, the speed of the body at point C is:
V=4g
The speed at point C, where the body passes at 4 seconds on the way up and 12 seconds on the way down, is 4g.
Similar Questions
A body thrown vertically upwards crosses a point p on its path after 2 seconds during its upward journey and again crosses the same point after 6 seconds during downward journey. Find the height of the point p from the ground (as a multiple of acceleration due to gravity)
View SolutionA body is falling freely under gravity. It passes two points A and B (A being higher than B) 20m apart vertically in 2s. Find the elevation of the point above A from where it began to fall.
View Solution
Knowledge Check
During upwards and downwards journeys under gravity, a body passes through a point at 2 s and 14 s. The total height from ground is
A4gB8gC16gD32gDuring upwards and downwards journeys under gravity, a body passes through a point at 2 s and 14 s. The total height from ground is
A4gB8gC16gD32gA particle is projected vertically upwards. What is the value of acceleration
(i) during upward journey,
(ii) during downward journey and
(iii) at highest point?A10 ms2B−10 ms2C10 ms2 −10 ms20 ms2DVariable
Read the given passage and answer the following questions.
A body is thrown vertically up with a velocity u as shown in the figure. It passes through points P and Q in its upward journey and reaches the maximum height at point R. Here PQPR=716,OP=2u245 , and take g=10m/s2
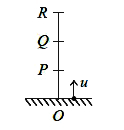
Find the velocity of the particle at point P.
View SolutionRead the given passage and answer the following questions.
A body is thrown vertically up with a velocity u as shown in the figure. It passes through points P and Q in its upward journey and reaches the maximum height at point R. Here PQPR=716,OP=2u245 , and take g=10m/s2
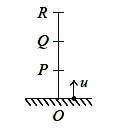
Find the time taken by the particle to reach highest point R.
View SolutionTwo balls of different masses are thrown vertically upwards with the same speed . They pass through the point of projection in their downward motion with the same speed ( Neglect air resistance ).
View SolutionA ball is thrown vertically up with a velocity u. It passes three points A,B and C in its upward journey with velocities us,u3 and u4, respectively. Find ABBC.
View SolutionAssertion In vertical circular motion, speed of a body cannot remain constant.
Reason In moving upwards, work done by gravity is negative.
View Solution

