The following data were obtained for the adsorptionof carbon monoxide gas on 3.0 g of charcoal at 0∘C and1 atm pressure.
Pressure (mmHg)200400Volume of gas adsorved,x18.631.4(reduced to STP)
Calculate the values of the constants k and n using Freundlich adsorption equation.
To solve the problem of calculating the constants k and n using the Freundlich adsorption equation, we will follow these steps:
Step 1: Write the Freundlich adsorption isotherm equation
The Freundlich adsorption isotherm equation is given by:
xm=k⋅p1n
Where:
- xm is the amount of adsorbate (gas) adsorbed per unit mass of adsorbent (charcoal).
- p is the pressure of the gas.
- k and n are constants.
Step 2: Convert the pressure from mmHg to atm
Given pressures are in mmHg, we need to convert them to atm for consistency with the conditions provided (1 atm = 760 mmHg).
- For 200mmHg:
p1=200760atm≈0.2632atm
- For 400mmHg:
p2=400760atm≈0.5263atm
Step 3: Calculate xm
The mass of charcoal is given as 3.0g.
- For 18.6cm3 of gas adsorbed:
xm1=18.63.0=6.2cm3/g
- For 31.4cm3 of gas adsorbed:
xm2=31.43.0=10.47cm3/g
Step 4: Take logarithms of both sides
Rearranging the Freundlich equation gives us:
log(xm)=log(k)+1nlog(p)
Using the two sets of data, we can form two equations:
1. For p1:
log(6.2)=log(k)+1nlog(0.2632)
2. For p2:
log(10.47)=log(k)+1nlog(0.5263)
Step 5: Solve the equations
Let’s denote:
- A=log(k)
- B1=log(0.2632)
- B2=log(0.5263)
Now we have:
1. log(6.2)=A+1nB1
2. log(10.47)=A+1nB2
Subtract the first equation from the second to eliminate A:
log(10.47)−log(6.2)=1n(B2−B1)
Step 6: Calculate the logarithms
Calculating the logarithms:
- log(6.2)≈0.7924
- log(10.47)≈1.0193
- B1≈−0.5770
- B2≈−0.2788
Substituting these values into the equation gives:
1.0193−0.7924=1n(−0.2788+0.5770)
Calculating the left side:
0.2269=1n(0.2982)
Step 7: Solve for n
Rearranging gives:
n=0.29820.2269≈1.31
Step 8: Substitute n back to find k
Now substitute n back into one of the original equations to find k:
Using the first equation:
log(6.2)=log(k)+11.31log(0.2632)
Calculating 11.31log(0.2632):
log(k)=0.7924−11.31(−0.5770)
Calculating the right side:
log(k)≈0.7924+0.4405≈1.2329
Thus,
k=101.2329≈17.0
Final Values
The values of the constants are:
- k≈17.0
- n≈1.31
The Freundlich adsorption isotherm equation is given by:
- xm is the amount of adsorbate (gas) adsorbed per unit mass of adsorbent (charcoal).
- p is the pressure of the gas.
- k and n are constants.
Given pressures are in mmHg, we need to convert them to atm for consistency with the conditions provided (1 atm = 760 mmHg).
p1=200760atm≈0.2632atm
p2=400760atm≈0.5263atm
The mass of charcoal is given as 3.0g.
xm1=18.63.0=6.2cm3/g
xm2=31.43.0=10.47cm3/g
Rearranging the Freundlich equation gives us:
log(6.2)=log(k)+1nlog(0.2632)
log(10.47)=log(k)+1nlog(0.5263)
Let’s denote:
- A=log(k)
- B1=log(0.2632)
- B2=log(0.5263)
1. log(6.2)=A+1nB1
2. log(10.47)=A+1nB2
Calculating the logarithms:
- log(6.2)≈0.7924
- log(10.47)≈1.0193
- B1≈−0.5770
- B2≈−0.2788
0.2269=1n(0.2982)
Rearranging gives:
n=0.29820.2269≈1.31
Now substitute n back into one of the original equations to find k:
log(6.2)=log(k)+11.31log(0.2632)
log(k)=0.7924−11.31(−0.5770)
log(k)≈0.7924+0.4405≈1.2329
k=101.2329≈17.0
The values of the constants are:
- k≈17.0
- n≈1.31
Topper's Solved these Questions
- SURFACE CHEMISTRYBook:MODERN PUBLICATIONChapter:SURFACE CHEMISTRYExercise:CONCEPTUAL QUESTION 1
Explore 14 Videos
- SURFACE CHEMISTRYBook:MODERN PUBLICATIONChapter:SURFACE CHEMISTRYExercise:CONCEPTUAL QUESTION 2
Explore 30 Videos
- SOLUTIONSBook:MODERN PUBLICATIONChapter:SOLUTIONSExercise:UNIT PRACTICE TEST
Explore 14 Videos
Similar Questions
The following data were obtained for the adsorption of CO on 3 g of charcoal at 0∘C
Pressuer (mm) : 180 540
Volume of gas absorbed in cc raduced to STP : 16.5 38.1
Calculate the values of the constants k and n used in Freundlich equation.
View SolutionThe following data were obtained for the adsorption of carbon monoxide gas on 3.022 g of charcoal at 0∘C and 1 atm pressure. Verify that the data obey the Langmuir monolyer adsorption isotherm. Also calculate the constant K and the volume (v) corresponding to complete surface coverege
P(toor):100200300400500600v(cm3):10.218.625.531.436.941.6
View Solution
Knowledge Check
The volume of 2.8g of carbon monoxide at 27∘C and 0.821atm pressure (R=0.821atmK−1mol−1)
A0.3LB1.5LC3LD30LA pure gas that is 14.3% hydrogen and 85.7% carbon by mass has a density of 2.5gL−1 at 0∘C and 1 atm pressure. What is the molecular formula of the gas :
ACH2BC2H4CC4H8DC6H12
The compression factor (compressibility factor) for 1mol of a van der Waals gas at 0∘C and 100atm pressure is found to be 0.5. Assuming that the volume of a gas molecule is neligible, calculate the van der Waals constant a.
View SolutionThe compression factor (compressibility factor) for 1mol of a van der Waals gas at 0∘C and 100atm pressure is found to be 0.5. Assuming that the volume of a gas molecule is neligible, calculate the van der Waals constant a.
View SolutionThe following data were obtained during the first order thermal
decomposition of SO2Cl2 at a constant volume SO2Cl2(g)→SO2(g)+Cl2(g)
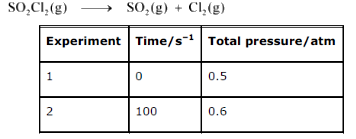
Calculate the rate of the reaction when total pressure is 0.65 atm
View SolutionIf 772 mL of SO2 gas at STP is adsorbed on 2 g of charcoal at an equilibrium pressure of 16 atmospheres and the value of the constant 'k' in the Freundlich equation is 0.48. the value of the constant 'n' will be
View SolutionThe following data were obtained the first order thermal decomposition of N2O5(g) at constant volume : 2N2O5(g)→2N2O4(g)+O2(g)
S. No.Time/sTotal pressure (atm)100.521000.512
Calculate the rate constant.
View SolutionThe following data were obtained during the first order thermal decomposition of N2O5 (g) at constant volume:
2N2O5(g)→2N2O4(g)+O2(g)
(S.no,Time,Total Pressure / atm),(1,0,0,5),(2,100,0.512)
Calculate the rate constant.
View Solution