The following data were obtained during the first order thermal decomposition of (g) at constant volume:
Calculate the rate constant.
To calculate the rate constant k for the first-order thermal decomposition of N2O5, we will follow these steps:
Step 1: Understand the Reaction
The reaction is given as:
2N2O5(g)→2N2O4(g)+O2(g)
Step 2: Set Up the Initial Conditions
At time t=0:
- Let the initial pressure of N2O5 be Pi.
- Given that the total pressure at t=0 is 0.5atm, we have:
Pi=0.5atm
Step 3: Analyze the Data at t=100s
At t=100s:
- The total pressure is Ptotal=0.512atm.
Step 4: Relate Total Pressure to Partial Pressures
From the stoichiometry of the reaction:
- For every 2 moles of N2O5 that decompose, 2 moles of N2O4 and 1 mole of O2 are produced.
- Let P be the change in pressure of N2O5 that decomposes. Then:
- Pressure of N2O5 at t=100s is Pi−2P
- Pressure of N2O4 at t=100s is 2P
- Pressure of O2 at t=100s is P
Thus, the total pressure at t=100s can be expressed as:
Ptotal=(Pi−2P)+2P+P=Pi+P
Step 5: Substitute Known Values
Substituting the known values:
0.512=0.5+P
Step 6: Solve for P
Rearranging gives:
P=0.512−0.5=0.012atm
Step 7: Calculate the Pressure of N2O5 at t=100s
Now, we can find the pressure of N2O5 at t=100s:
PN2O5=Pi−2P=0.5−2(0.012)=0.5−0.024=0.476atm
Step 8: Use the First-Order Rate Constant Formula
For a first-order reaction, the rate constant k can be calculated using the formula:
k=2.303tlog(PiPN2O5)
Substituting the values:
- t=100s
- Pi=0.5atm
- PN2O5=0.476atm
Step 9: Calculate k
k=2.303100log(0.50.476)
Calculating the logarithm:
log(0.50.476)≈log(1.0504)≈0.021
Now substituting back:
k=2.303100×0.021≈4.92×10−4s−1
Final Answer
The rate constant k for the first-order thermal decomposition of N2O5 is approximately:
k≈4.92×10−4s−1
---
The reaction is given as:
2N2O5(g)→2N2O4(g)+O2(g)
At time t=0:
- Let the initial pressure of N2O5 be Pi.
- Given that the total pressure at t=0 is 0.5atm, we have:
Pi=0.5atm
At t=100s:
- The total pressure is Ptotal=0.512atm.
From the stoichiometry of the reaction:
- For every 2 moles of N2O5 that decompose, 2 moles of N2O4 and 1 mole of O2 are produced.
- Let P be the change in pressure of N2O5 that decomposes. Then:
- Pressure of N2O5 at t=100s is Pi−2P
- Pressure of N2O4 at t=100s is 2P
- Pressure of O2 at t=100s is P
Ptotal=(Pi−2P)+2P+P=Pi+P
Substituting the known values:
0.512=0.5+P
Rearranging gives:
P=0.512−0.5=0.012atm
Now, we can find the pressure of N2O5 at t=100s:
PN2O5=Pi−2P=0.5−2(0.012)=0.5−0.024=0.476atm
For a first-order reaction, the rate constant k can be calculated using the formula:
k=2.303tlog(PiPN2O5)
- t=100s
- Pi=0.5atm
- PN2O5=0.476atm
k=2.303100log(0.50.476)
log(0.50.476)≈log(1.0504)≈0.021
k=2.303100×0.021≈4.92×10−4s−1
The rate constant k for the first-order thermal decomposition of N2O5 is approximately:
k≈4.92×10−4s−1
Topper's Solved these Questions
- CHEMICAL KINETICS Book:NARAYNAChapter:CHEMICAL KINETICS Exercise:EVALUATE YOURSELF - 1
Explore 2 Videos
- CHEMICAL KINETICS Book:NARAYNAChapter:CHEMICAL KINETICS Exercise:EVALUATE YOURSELF - 2
Explore 3 Videos
- CARBOXYLIC ACIDBook:NARAYNAChapter:CARBOXYLIC ACIDExercise:All Questions
Explore 288 Videos
- CHEMISTRY IN EVERYDAY LIFEBook:NARAYNAChapter:CHEMISTRY IN EVERYDAY LIFEExercise:ASSERTION & REASON TYPE QUESTIONS
Explore 10 Videos
Similar Questions
The following data were obtained during the first thermal decompoistion of N2O5(g) at constant volume.
2N2O5(g)→2N2O4(g)+O2(g)
∣∣ ∣ ∣∣S.No.Time (s)Total pressure (atm)i.00.5ii.1000.512∣∣ ∣ ∣∣
Calculate the rate constant.
View SolutionThe following data were obtained the first order thermal decomposition of N2O5(g) at constant volume : 2N2O5(g)→2N2O4(g)+O2(g)
S. No.Time/sTotal pressure (atm)100.521000.512
Calculate the rate constant.
View Solution
Knowledge Check
The following data were obtained during the first order thermal decomposition of SO2CI2 at a constant volume.
SO2CI2(g)→SO2(g)+CI2(g)
ExperimentTime/s−1Total pressure/atm100.521000.6
What is the rate of reaction when total pressure is 0.65 atm?A0.35atms−1B2.235×10−3atms−1C7.8×10−4atms−1D1.55×10−4atms−1The following data were obtained during the first order thermal
decomposition of SO2Cl2 at a constant volume SO2Cl2(g)→SO2(g)+Cl2(g)
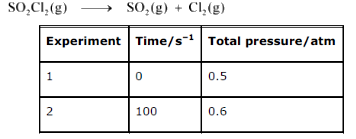
Calculate the rate of the reaction when total pressure is 0.65 atmA0.35atmS−1B2.235×10−3atmS−1C7.8×10−4atms−1D1.55×10−4atmS−1
The following data were obtained during the first order thermal decomposition of N2O5 at constant volume :
2N2O5→2N2O4+O2

Calculate rate constant.
View SolutionThe following data were obtained during the first order thermal decomposition of N2O5(g) at constant volume.
2N2O5(g)→2N2O2(g)+O2(g)

Calculate the rate constant for the gaseous reaction.
View SolutionThe following data were obtained during the first order thermal decomposition of SO2Cl2 at a constant volume :
SO2Cl2(g)→SO2(g)+Cl2(g)
Experiment Times/s−1 Total pressure/atm1 0 0.42 100 0.7
Calculate the rate constant. Given : log 4 = 0.6021, log 2 = 0.3010)
View SolutionThe following data were obtained during the first order thermal
decomposition of SO2Cl2 at a constant volume SO2Cl2(g)→SO2(g)+Cl2(g)

Calculate the rate of the reaction when total pressure is 0.65 atm
View SolutionThe following data were obtained during the first order decomposition of SO2Cl2 at a constant volume:
SO2Cl2(g)→SO2(g)+Cl2(g)

Calculate the rate constant.
View SolutionThe following data were obtained during the first order thermal
decomposition of SO2Cl2 at a constant volume SO2Cl2(g)→SO2(g)+Cl2(g)

Calculate the rate of the reaction when total pressure is 0.65 atm
View Solution

