The following data were obtained the first order thermal decomposition of N2O5(g) at constant volume : 2N2O5(g)→2N2O4(g)+O2(g)
S. No.Time/sTotal pressure (atm)100.521000.512
Calculate the rate constant.
To calculate the rate constant for the first-order thermal decomposition of N2O5(g), we will follow these steps:
Step 1: Write the reaction and understand the initial conditions
The reaction is:
2N2O5(g)→2N2O4(g)+O2(g)
At time t=0:
- Total pressure P0=0.5atm
Step 2: Define the change in pressure
Let x be the change in pressure due to the decomposition of N2O5. The stoichiometry of the reaction indicates that for every 2 moles of N2O5 that decompose, 2 moles of N2O4 and 1 mole of O2 are produced.
At time t:
- Pressure of N2O5=P0−2x
- Pressure of N2O4=2x
- Pressure of O2=x
Step 3: Use the total pressure at t=100s
Given total pressure at t=100s is Pt=0.512atm.
The total pressure at time t can be expressed as:
Pt=(P0−2x)+2x+x
Pt=P0+x
Substituting the values:
0.512=0.5+x
Thus,
x=0.512−0.5=0.012atm
Step 4: Calculate the pressure of N2O5 at t=100s
Now we can find the pressure of N2O5:
PN2O5=P0−2x=0.5−2(0.012)=0.5−0.024=0.476atm
Step 5: Use the first-order rate constant formula
For a first-order reaction, the rate constant k can be calculated using the formula:
k=2.303tlog(PinitialPfinal)
Substituting the values:
- Pinitial=0.5atm
- Pfinal=0.476atm
- t=100s
k=2.303100log(0.50.476)
Step 6: Calculate the logarithm
Calculate the logarithm:
log(0.50.476)=log(1.05042)≈0.021
Step 7: Calculate k
Now substituting back:
k=2.303100×0.021
k≈0.0483100
k≈4.83×10−4s−1
Final Answer
The rate constant k for the decomposition of N2O5 is approximately:
k≈4.83×10−4s−1
---
The reaction is:
2N2O5(g)→2N2O4(g)+O2(g)
- Total pressure P0=0.5atm
Let x be the change in pressure due to the decomposition of N2O5. The stoichiometry of the reaction indicates that for every 2 moles of N2O5 that decompose, 2 moles of N2O4 and 1 mole of O2 are produced.
- Pressure of N2O5=P0−2x
- Pressure of N2O4=2x
- Pressure of O2=x
Given total pressure at t=100s is Pt=0.512atm.
Pt=(P0−2x)+2x+x
Pt=P0+x
0.512=0.5+x
Thus,
x=0.512−0.5=0.012atm
Now we can find the pressure of N2O5:
PN2O5=P0−2x=0.5−2(0.012)=0.5−0.024=0.476atm
For a first-order reaction, the rate constant k can be calculated using the formula:
k=2.303tlog(PinitialPfinal)
- Pinitial=0.5atm
- Pfinal=0.476atm
- t=100s
Calculate the logarithm:
log(0.50.476)=log(1.05042)≈0.021
Now substituting back:
k=2.303100×0.021
k≈0.0483100
k≈4.83×10−4s−1
The rate constant k for the decomposition of N2O5 is approximately:
k≈4.83×10−4s−1
Topper's Solved these Questions
- CHEMICAL KINETICSBOOK - PRADEEPCHAPTER - CHEMICAL KINETICSEXERCISE - PROBLEMS FOR PRACTICE
73 Videos
- CHEMICAL KINETICSBOOK - PRADEEPCHAPTER - CHEMICAL KINETICSEXERCISE - CURIOSITY QUESTION
2 Videos
- BIOMOLECULES BOOK - PRADEEPCHAPTER - BIOMOLECULES EXERCISE - IMPORTANT QUESTIONS (FOR BOARD EXAMINATION)
25 Videos
- CHEMISTRY IN EVERYDAY LIFE BOOK - PRADEEPCHAPTER - CHEMISTRY IN EVERYDAY LIFE EXERCISE - IMPORTANT QUESTION FOR BOARD EXAMINATION
30 Videos
Similar Questions
The following data were obtained during the first order thermal decomposition of N2O5 (g) at constant volume:
2N2O5(g)→2N2O4(g)+O2(g)
(S.no,Time,Total Pressure / atm),(1,0,0,5),(2,100,0.512)
Calculate the rate constant.
View SolutionThe following data were obtained during the first thermal decompoistion of N2O5(g) at constant volume.
2N2O5(g)→2N2O4(g)+O2(g)
∣∣ ∣ ∣∣S.No.Time (s)Total pressure (atm)i.00.5ii.1000.512∣∣ ∣ ∣∣
Calculate the rate constant.
View Solution
Knowledge Check
The following data were obtained during the first order thermal
decomposition of SO2Cl2 at a constant volume SO2Cl2(g)→SO2(g)+Cl2(g)
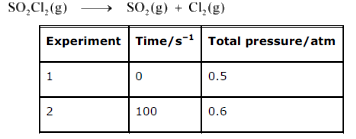
Calculate the rate of the reaction when total pressure is 0.65 atmA0.35atmS−1B2.235×10−3atmS−1C7.8×10−4atms−1D1.55×10−4atmS−1The following data were obtained during the first order thermal decomposition of SO2CI2 at a constant volume.
SO2CI2(g)→SO2(g)+CI2(g)
ExperimentTime/s−1Total pressure/atm100.521000.6
What is the rate of reaction when total pressure is 0.65 atm?A0.35atms−1B2.235×10−3atms−1C7.8×10−4atms−1D1.55×10−4atms−1
The following data were obtained during the first order thermal
decomposition of SO2Cl2 at a constant volume SO2Cl2(g)→SO2(g)+Cl2(g)

Calculate the rate of the reaction when total pressure is 0.65 atm
View SolutionThe following data were obtained during the first order thermal decomposition of N2O5 at constant volume :
2N2O5→2N2O4+O2

Calculate rate constant.
View SolutionThe following data were obtained during the first order thermal decomposition of N2O5(g) at constant volume.
2N2O5(g)→2N2O2(g)+O2(g)

Calculate the rate constant for the gaseous reaction.
View SolutionThe following data were obtained during the first order thermal decomposition of SO2Cl2 at a constant volume :
SO2Cl2(g)→SO2(g)+Cl2(g)
Experiment Times/s−1 Total pressure/atm1 0 0.42 100 0.7
Calculate the rate constant. Given : log 4 = 0.6021, log 2 = 0.3010)
View SolutionThe following data were obtained during the first order decomposition of SO2Cl2 at a constant volume:
SO2Cl2(g)→SO2(g)+Cl2(g)

Calculate the rate constant.
View SolutionThe following data were obtained during the first order thermal
decomposition of SO2Cl2 at a constant volume SO2Cl2(g)→SO2(g)+Cl2(g)

Calculate the rate of the reaction when total pressure is 0.65 atm
View Solution
