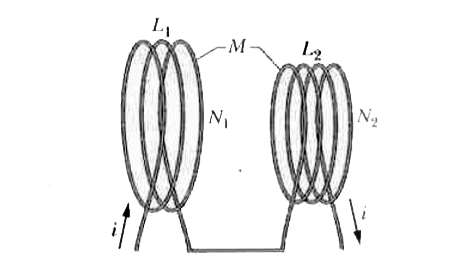
In Fig. coil $1$ and coil $2$ are wound on a long cylindrical insulator. The ends $A'$ and $B$ are joined together and current $I$ is passed. Self-inductance of the two coils are $L_{1}$ and $L_{2}$ , and their mutual inductance is $M$ .
a. Show that this combination can be replaced by a single coil of equivalent inductanCe given by
$L_{e q} = L_{1} + L_{2} + 2 M$ .
b. How could the coils be reconnected by yieldings an equivalent inductance of $L_{e q} = L_{1} + L_{2} - 2 M$ .

Video Solution

Text Solution

Verified by Experts

The emf induced across coil BB. must be
$V_{B} = - L_{B} \frac{d i_{B}}{d t} + M \frac{d i_{A}}{d t}$
Note that the magnetic field due to the coil itself and due to coil AA. are in opposite directions. So, their induced emf will also have opposite signs. Here M is the (magnitude of the) mutual inductance between the coils. Since the coils are connected in series $i_{A} = i_{B} = i$ , so that
$V_{B} = - (L_{B} - M) \frac{d i}{d t}$
Similarly, we find that the emf induced across coil AA.is
$V_{A} = - (L_{A} - M) \frac{d i}{d t}$
The emf across the entire series coil assembly is the sum of $V_{A}$ and $V_{B}$ :
$V = V_{A} + V_{B} = - (L_{A} + L_{B} - 2 M) \frac{d i}{d t}$

Updated on:21/07/2023

Mutual inductance of two coils depends on their self inductance $L_{1}$ and $L_{2}$ as :
A $M_{12} = L_{1} / L_{2}$
B $M_{12} = L_{2} / L_{1}$
C $M_{12} = \sqrt{L_{1} L_{2}}$
D $M_{12} = \sqrt{L_{1} / L_{2}}$
The self-inductances of two identical coils are 0.1H. They are wound over each other. Mutual inductance will be-
A0.1H
B0.2H
C0.01H
D0.05H
The mutual inductance $M_{12}$ of coil 1 with respect to coil 2
Aincreases when they are brought nearer
Bdepends on the current passing through the coils
Cincreases when one of them is rotated about an axis
Dis the same as $M_{21}$ coil 2 with respect to coil 1