A uniform magnetic flux density of 0.1 Wb/m extends over a plane circuit of area 2 m2 and is normal to it. How quickly must the field be reduced to zero, if an emf of 100 V is to be induced in the circuit?
The correct Answer is:B
To solve the problem, we need to calculate how quickly the magnetic field must be reduced to zero in order to induce an emf of 100 V in the circuit. We will use Faraday's law of electromagnetic induction, which states that the induced emf (E) in a closed loop is equal to the negative rate of change of magnetic flux (Φ) through the loop.
1. Identify the Given Values:
- Magnetic flux density (B) = 0.1 Wb/m²
- Area of the circuit (A) = 2 m²
- Induced emf (E) = 100 V
2. Calculate the Initial Magnetic Flux (Φ_initial):
The magnetic flux (Φ) through the circuit is given by the formula:
Φ=B⋅A
Substituting the values:
Φinitial=0.1Wb/m²×2m²=0.2Wb
3. Determine the Final Magnetic Flux (Φ_final):
Since we want to reduce the magnetic field to zero, the final magnetic flux will be:
Φfinal=0Wb
4. Calculate the Change in Magnetic Flux (ΔΦ):
The change in magnetic flux is:
ΔΦ=Φfinal−Φinitial=0−0.2=−0.2Wb
5. Apply Faraday's Law:
According to Faraday's law:
E=−dΦdt
Rearranging gives:
dt=−dΦE
Substituting the values:
dt=−−0.2Wb100V=0.2100=0.002s
6. Convert Time to Milliseconds:
dt=0.002s=2ms
Final Answer:
The magnetic field must be reduced to zero in 2 milliseconds to induce an emf of 100 V in the circuit.
- Magnetic flux density (B) = 0.1 Wb/m²
- Area of the circuit (A) = 2 m²
- Induced emf (E) = 100 V
The magnetic flux (Φ) through the circuit is given by the formula:
Φ=B⋅A
Substituting the values:
Φinitial=0.1Wb/m²×2m²=0.2Wb
Since we want to reduce the magnetic field to zero, the final magnetic flux will be:
Φfinal=0Wb
The change in magnetic flux is:
ΔΦ=Φfinal−Φinitial=0−0.2=−0.2Wb
According to Faraday's law:
E=−dΦdt
Rearranging gives:
dt=−dΦE
Substituting the values:
dt=−−0.2Wb100V=0.2100=0.002s
dt=0.002s=2ms
The magnetic field must be reduced to zero in 2 milliseconds to induce an emf of 100 V in the circuit.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:RESNICK AND HALLIDAYChapter:ELECTROMAGNETIC INDUCTIONExercise:PRACTICE QUESTIONS (Matrix-Match)
Explore 8 Videos
- ELECTRIC POTENTIALBook:RESNICK AND HALLIDAYChapter:ELECTRIC POTENTIALExercise:(PRACTICE QUESTIONS) Integer Type
Explore 1 Video
- ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT Book:RESNICK AND HALLIDAYChapter:ELECTROMAGNETIC OSCILLATIONS AND ALTERNATING CURRENT Exercise:Practice Questions (Integer)
Explore 7 Videos
Similar Questions
A magnetic field of flux density 1.0 Wb/m2 acts normal to an 80 tum coil of 0.01 m2 area. Find the emf induced in it, if this coil is removed from the field in 0.1 s.
View SolutionA magnetic field of flux density 10 T act normal to a 50 turn coil of 100cm2 area. Find the emf induced in it if the coil is removed from the field in 1/20 s.
View Solution
Knowledge Check
A coil of area 0.4m2 has 100 turns. A magnetic field of 0.04Wb/m−2 is acting normal to the coil surface. If this magnetic field is reduced to zero in 0.01 s, then the induced emf in the coil is
A160VB250 VC270 VD320 VA coil of area 10 cm2 has 200 turns. Magnetic field of 0.1 Wb/m2 is perpendicular to the plane of the coil. The field is reduced to zero in 0.1 s, the induced emf in the coil is
A1VB0.2VC2VD0A proton enters a magnetic field of flux density 1.5Wb/m2 with a velocity of 2×10−7 m/s at an angle of 30∘ with the field. The force on the proton will be
A2.4×10−12NB0.24×10−12NC24×10−12ND0.024×10−12N
A magnetic field of flux density 10 T acts normal to a coil of 50 turns having 20cm2 area. Find emf induced if the coil is removed from the magnetic field in 0.1 sec.
View SolutionA 0.5m long metal rod PQ completes the circuit as shown in the figure. The area of the circuit is perpendicular to the magnetic field of flux density 0.15T. If the resistance of the total circuit is 3Ω calculate the force needed to move the rod in the direction as indicated with a constant speed of 2ms−1
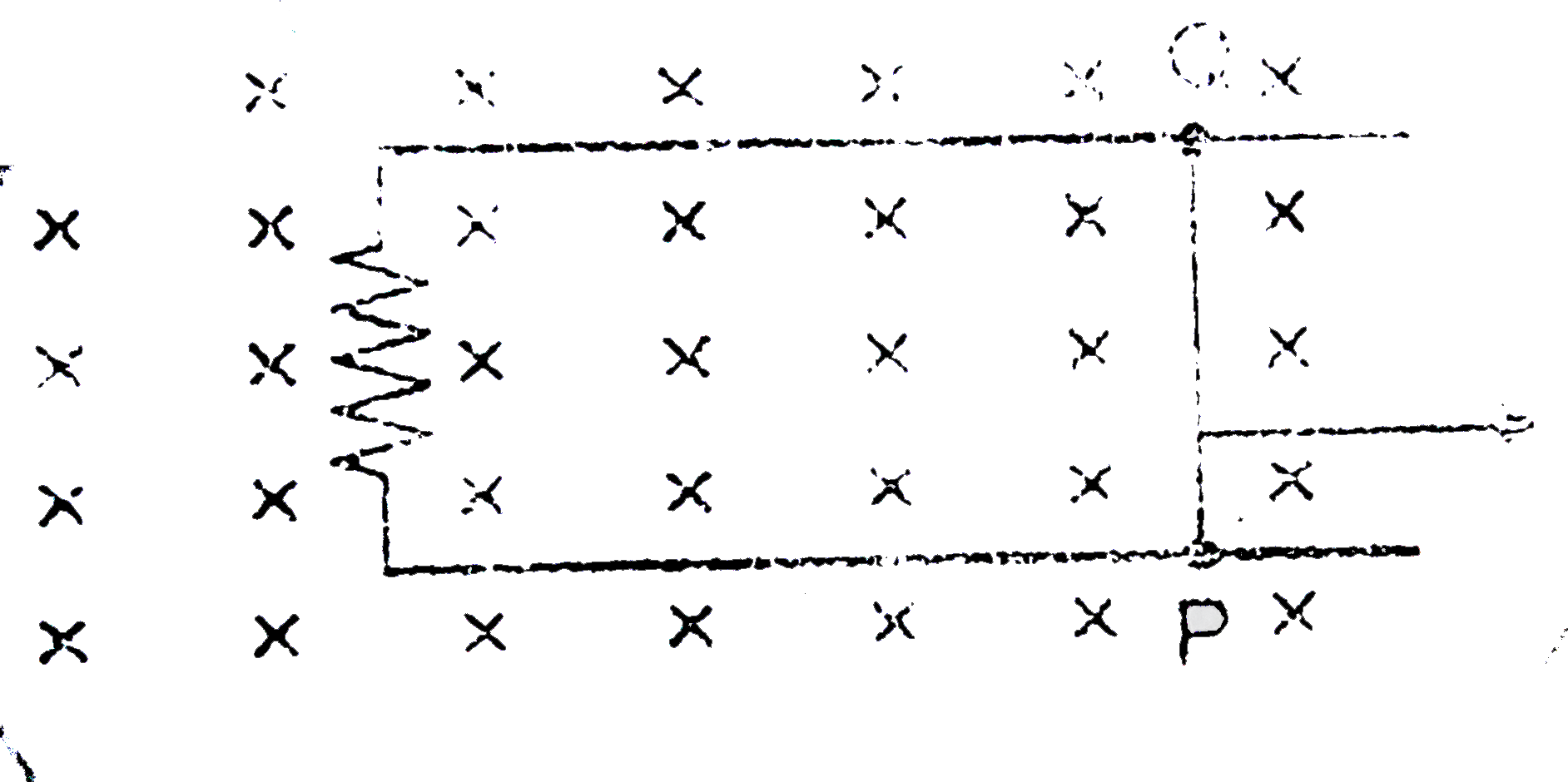
View SolutionA rectangular loop (area = 0.15 m2) turns in a uniform magnetic field, B = 0.20 T. When the angle between the field and the normal to the plane of the loop is π/2 rad and increasing at 0.60 rad/s, what emf is induced in the loop?
View SolutionCurrent in a circuit falls form 0.5 A to 0.0 A in 0.1 s. If an average e.m.f. of 200 V is induced, give an estimate of the self inductance of the circuit ?
View SolutionA coil of area 100cm2 has 500 turns. Magnetic field of 0.1weber/meter2 is perpendicular to the coil. The field is reduced to zero in 0.1 second. The induced e.m.f. in the coil is
View Solution
