Question

Induced emf due to a changing nonuniform B field
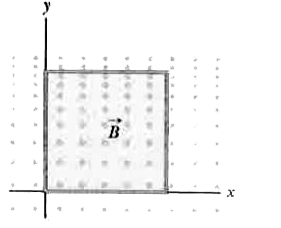
Figure 30-9 shows a rectangular loop of wire immersed in a nonuniform and varying magnetic field $\overrightarrow{B}$ that is perpendicular to and directed into the page. The field's magnitude is given by $B=4t^2{x}^2$, with B in teslas, tin seconds, and x in meters. (Note that the function depends on both time and position.) The loop has width W = 3.0 m and height H = 2.0 m. What are the magnitude and direction of the induced emf E around the loop at t = 0.10 s?

Explanation

To find the induced emf (E) around the loop at t = 0.10 s due to a nonuniform magnetic field, we will follow these steps:

Step 1: Understand the Problem
The magnetic field is given by \( B = 4t^2 x^2 \), where \( B \) is in teslas, \( t \) is in seconds, and \( x \) is in meters. The loop has a width \( W = 3.0 \, \text{m} \) and height \( H = 2.0 \, \text{m} \).

Step 2: Calculate the Magnetic Flux
The magnetic flux \( \Phi \) through the loop is given by the integral of the magnetic field over the area of the loop. The area element \( dA \) can be expressed as \( dA = H \cdot dx \), where \( H \) is the height of the loop and \( dx \) is an infinitesimal width.

Thus, the total flux \( \Phi \) through the loop is:
\( \Phi = \int_0^W B \, dA = \int_0^W B \cdot H \, dx \)
Substituting \( B = 4t^2 x^2 \):
\( \Phi = \int_0^W 4t^2 x^2 H \, dx \)

Step 3: Evaluate the Integral
Now, we can evaluate the integral:
\( \Phi = 4t^2 H \int_0^W x^2 \, dx \)
The integral of \( x^2 \) from 0 to \( W \) is:
\( \int_0^W x^2 \, dx = \left( \frac{x^3}{3} \right)_0^W = \frac{W^3}{3} \)
Thus, substituting this back into the equation for flux:
\( \Phi = 4t^2 H \cdot \frac{W^3}{3} \)

Step 4: Differentiate the Flux to Find Induced EMF
According to Faraday's law of electromagnetic induction, the induced emf \( E \) is given by:
\( E = -\frac{d\Phi}{dt} \)
Now we differentiate \( \Phi \):
\( E = -\frac{d}{dt} \left( 4t^2 H \cdot \frac{W^3}{3} \right) \)
Taking the derivative:
\( E = -\left( 4H \cdot \frac{W^3}{3} \cdot \frac{d}{dt}(t^2) \right) = -\left( 4H \cdot \frac{W^3}{3} \cdot 2t \right) \)
Thus:
\( E = -\frac{8HtW^3}{3} \)

Step 5: Substitute Values
Now, we substitute \( H = 2.0 \, \text{m} \), \( W = 3.0 \, \text{m} \), and \( t = 0.1 \, \text{s} \):
\( E = -\frac{8 \cdot 2 \cdot 0.1 \cdot (3)^3}{3} \)
Calculating \( (3)^3 = 27 \):
\( E = -\frac{8 \cdot 2 \cdot 0.1 \cdot 27}{3} = -\frac{432 \cdot 0.1}{3} = -\frac{43.2}{3} = -14.4 \, \text{V} \)

Step 6: Determine the Magnitude and Direction
The magnitude of the induced emf is:
\( |E| = 14.4 \, \text{V} \)
The negative sign indicates that the induced emf opposes the change in magnetic flux (Lenz's law).

Final Answer
The magnitude of the induced emf around the loop at \( t = 0.10 \, \text{s} \) is \( 14.4 \, \text{V} \), and the direction is such that it opposes the change in magnetic flux.

---