A helicopter, at an altitude of 1500 metre, finds that two ships are sailing towards it, in the same direction. The angles of depression of the ships as observed from the helicopter are respectively. Distance between the two ships, in metre is
The correct Answer is:A
To solve the problem, we need to find the distance between two ships observed from a helicopter at an altitude of 1500 meters, given the angles of depression to the ships are 60° and 30° respectively.
1. Understand the Geometry:
- Let the helicopter be at point A, the first ship at point D, and the second ship at point E.
- The altitude of the helicopter (AC) is 1500 meters.
- The angles of depression to the ships are 60° (for ship D) and 30° (for ship E).
2. Draw the Right Triangles:
- From point A (helicopter), draw a vertical line down to point C (the ground directly below A).
- Draw horizontal lines from C to D and C to E, forming right triangles ACD and ACE.
3. Using Trigonometry for Ship D:
- In triangle ACD, where angle CAD = 60°:
tan(60°)=ACCD
√3=1500CD
CD=1500√3=500√3 meters
4. Using Trigonometry for Ship E:
- In triangle ACE, where angle CAE = 30°:
tan(30°)=ACCE
1√3=1500CE
CE=1500√3 meters
5. Finding the Distance Between the Two Ships:
- The distance DE between the two ships can be found by subtracting the distances from C to D and C to E:
DE=CE−CD
DE=1500√3−500√3=(1500−500)√3=1000√3 meters
Final Answer:
The distance between the two ships is 1000√3 meters.
- Let the helicopter be at point A, the first ship at point D, and the second ship at point E.
- The altitude of the helicopter (AC) is 1500 meters.
- The angles of depression to the ships are 60° (for ship D) and 30° (for ship E).
- From point A (helicopter), draw a vertical line down to point C (the ground directly below A).
- Draw horizontal lines from C to D and C to E, forming right triangles ACD and ACE.
- In triangle ACD, where angle CAD = 60°:
tan(60°)=ACCD
√3=1500CD
CD=1500√3=500√3 meters
- In triangle ACE, where angle CAE = 30°:
tan(30°)=ACCE
1√3=1500CE
CE=1500√3 meters
- The distance DE between the two ships can be found by subtracting the distances from C to D and C to E:
DE=CE−CD
DE=1500√3−500√3=(1500−500)√3=1000√3 meters
The distance between the two ships is 1000√3 meters.
Similar Questions
An aeroplane at an altitude of 1200 metres finds that two ships are sailing towards it in the same direction. The angles of depression of the ships as observed from the aeroplane are 60o and 30o respectively. Find the distance between the two ships.
View SolutionTwo ships are there in the sea on either side of a light house in such a way that the ships and the light house are in the same straight line. The angles of depression of two ships are observed from the top of the light house are 60o and 45o respectively. If the height of the light house is 200 m, find the distance between the two ships. (Use √3=1.73)
View Solution
Knowledge Check
An observer standing on a 300 m high tower observes two boats in the same direction, their angle of depression are 60∘and30∘ respectively. The distance between the boats is
A173.2 mB346.4 mC25 mD72 mTwo ships A and B are sailing straight away from the foot of a tower OP along routes such that ∣AOB––––––– is always 120∘. At a certain instance, the angles of depression of the ships A and B from the top P of the towers are 60∘and30∘ respectively. The distance between the ships when the height of the tower is 15m is
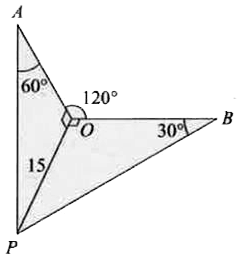 A5√39 mB5√30 mC5√21 mD5√3 m
A5√39 mB5√30 mC5√21 mD5√3 mTwo ships are sailing in the sea on either side of a light -house . The angle of depression of the two ships are 45∘ each . If the height of the light-house is 300 metres, then the distance between the ships is
A600 mB600/√3mC300√3mD300 m
Two ships are sailing in the sea on the either side of the lighthouse.The angles of depression of two ships as observed from the top of the lighthouse are 60∘ and 45∘, respectively. If the distance between the ships is 100(√3+1√3) m, then find the height of the lighthouse
View SolutionThe angle of depression of a ship from the top a tower of height 50 m is 30∘. Find the horizontal distance between the ship and tower.
View SolutionAn army from the top of a 75 m high light house from the sea level, observes some suspicious activities of two ships which are sailing towards it and immediately reports it to the navy chief. The angle of depression of two ships are 45∘ and 30∘ respectively.
(i) Find the distance between the two ships.
(ii) What value of the army is shown here ?
View SolutionThe angle if depression of a ship from the top a tower of height 50 m is 30∘. Find the horizontal distance between the boat and the bridge.
View SolutionThe cliff a mountain is 180 m high and the angles of depression of two ships on the either side of cliff are 30∘and60∘ .What is the distance between the tow ships ?
View Solution