RENT is a rectangle (Fig 3.41). Its diagonals meet at O. Find x, if OR=2x+4andOT=3x+1
To solve the problem, we will use the property of rectangles that states the diagonals bisect each other and are equal in length. This means that the segments formed by the diagonals at the intersection point (point O) are equal.
Given:
- OR=2x+4
- OT=3x+1
Since OR and OT are segments of the diagonals that meet at point O, we can set them equal to each other:
1. Set the equations equal to each other:
OR=OT
2x+4=3x+1
2. Rearrange the equation:
To isolate x, we will first move all terms involving x to one side and constant terms to the other side. Subtract 2x from both sides:
4=3x−2x+1
This simplifies to:
4=x+1
3. Solve for x:
Now, subtract 1 from both sides:
4−1=x
x=3
Thus, the value of x is 3.
- OR=2x+4
- OT=3x+1
OR=OT
2x+4=3x+1
To isolate x, we will first move all terms involving x to one side and constant terms to the other side. Subtract 2x from both sides:
4=3x−2x+1
This simplifies to:
4=x+1
Now, subtract 1 from both sides:
4−1=x
x=3
Topper's Solved these Questions
- UNDERSTANDING QUADRILATERALSBOOK - NCERTCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.2
6 Videos
- UNDERSTANDING QUADRILATERALSBOOK - NCERTCHAPTER - UNDERSTANDING QUADRILATERALSEXERCISE - EXERCISE 3.3
11 Videos
- SQUARES AND SQUARE ROOTSBOOK - NCERTCHAPTER - SQUARES AND SQUARE ROOTSEXERCISE - EXERCISE 6.1
9 Videos
- VISUALISING SOLID SHAPESBOOK - NCERTCHAPTER - VISUALISING SOLID SHAPESEXERCISE - EXERCISE 10.3
8 Videos
Similar Questions
In Figure, RENT is a rectangle. Its diagonals meet at O. Find x, if OR=2x+4 and OT=3x+1.
View SolutionRENT is a rectangle. Its diagonals meets at O. Find x if OR=2x+3 and OT=3x+2.
View SolutionROCK is a rectangle. Its diagonals meet at A. Find a if RA=4a−5 and OA=3a+3.

View SolutionIn the figure, HOPE is a rectangle. Its diagonals meet at G. If HG = 5x + 1 and EG = 4x + 19, find x.

View SolutionThe diagonals of a rectangle ABCD meet at O . If ∠BOC=44∘, find ∠OAD
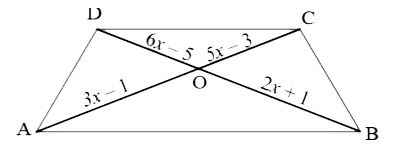
View SolutionIn the given fig., AB || DC and diagonals AC and BD intersects at O. If OA =3x-1 and OB =2x + 1, OC = 5x-3 and OD =6x-5, find the value of x.
View SolutionFind the equation of the circle drawn on the diagonals of the rectangle as its diameter whose sides are :
(i) x = 6 , x = - 3, y = 3 and y = - 1
(ii) x = 5 , x = 8 , y = 4 , y = 7 .
View SolutionThe diagonals of a rectangle ABCD meet at O. If ∠BOC=44∘, find ∠OAD.
View SolutionThe diagonals of a rectangle ABCD meet at O. If ∠BOC=440, find ∠OAD.
View SolutionThe equation of one side of a rectangle is 3x−4y−10=0 and the coordinates of two of its vertices are (−2,1)and(2,4). Find the area of the rectangle and the equation of that diagonal of the rectangle which passes through the point (2,4).
View Solution
