Two conducting concentric spherical shells are given positive charges. Choose the correct outcome.
Outer shell will be at higher potential
Inner shell will be at higher potential
Outer will always be at higher potential irrespective of the sign of charges given to two spheres
No prediction can be made using the given data
The correct Answer is:B
To solve the problem of determining which conducting spherical shell has a higher electric potential when both are given positive charges, we can follow these steps:
Step 1: Understand the Setup
We have two concentric spherical shells:
- Inner shell with radius R1 and charge Q1
- Outer shell with radius R2 and charge Q2
Step 2: Define the Charges
Let:
- Q1=Q (charge on the inner shell)
- Q2=Q (charge on the outer shell)
Step 3: Calculate the Potential on the Inner Shell
The potential Vi at the surface of the inner shell due to its own charge is given by:
Vi=kQR1
where k is Coulomb's constant.
Additionally, the potential at the inner shell due to the outer shell (which acts as a point charge from the perspective of the inner shell) is:
Vouter=kQR2
Thus, the total potential Vinner at the inner shell is:
Vinner=Vi+Vouter=kQR1+kQR2
Step 4: Calculate the Potential on the Outer Shell
The potential Vo at the surface of the outer shell due to its own charge is:
Vo=kQR2
The potential at the outer shell due to the inner shell is:
Vinner=kQR1
Thus, the total potential Vouter at the outer shell is:
Vouter=Vo+Vinner=kQR2+kQR1
Step 5: Compare the Potentials
Now, we compare Vinner and Vouter:
- Vinner=kQR1+kQR2
- Vouter=kQR2+kQR1
Since both expressions are equal, we need to analyze the terms:
- The potential due to the inner shell is higher because R1<R2.
Conclusion
Since R1<R2, it follows that:
Vinner>Vouter
Thus, the inner shell has a higher potential than the outer shell.
Final Answer
The inner shell will be at a higher potential.
---
We have two concentric spherical shells:
- Inner shell with radius R1 and charge Q1
- Outer shell with radius R2 and charge Q2
Let:
- Q1=Q (charge on the inner shell)
- Q2=Q (charge on the outer shell)
The potential Vi at the surface of the inner shell due to its own charge is given by:
Vi=kQR1
where k is Coulomb's constant.
Vouter=kQR2
Thus, the total potential Vinner at the inner shell is:
Vinner=Vi+Vouter=kQR1+kQR2
The potential Vo at the surface of the outer shell due to its own charge is:
Vo=kQR2
The potential at the outer shell due to the inner shell is:
Vinner=kQR1
Thus, the total potential Vouter at the outer shell is:
Vouter=Vo+Vinner=kQR2+kQR1
Now, we compare Vinner and Vouter:
- Vinner=kQR1+kQR2
- Vouter=kQR2+kQR1
- The potential due to the inner shell is higher because R1<R2.
Since R1<R2, it follows that:
Vinner>Vouter
Thus, the inner shell has a higher potential than the outer shell.
The inner shell will be at a higher potential.
Topper's Solved these Questions
- ELECTRIC POTENTIALBook:RESNICK AND HALLIDAYChapter:ELECTRIC POTENTIALExercise:(PRACTICE QUESTIONS) More than One Correct Choice Type
Explore 8 Videos
- ELECTRIC POTENTIALBook:RESNICK AND HALLIDAYChapter:ELECTRIC POTENTIALExercise:(PRACTICE QUESTIONS) Linked Comprehension
Explore 2 Videos
- ELECTRIC POTENTIALBook:RESNICK AND HALLIDAYChapter:ELECTRIC POTENTIALExercise:(PROBLEMS)
Explore 47 Videos
- ELECTRIC CHARGES AND FIELDSBook:RESNICK AND HALLIDAYChapter:ELECTRIC CHARGES AND FIELDSExercise:Practice Questions (Integer Type )
Explore 3 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESNICK AND HALLIDAYChapter:ELECTROMAGNETIC INDUCTIONExercise:PRACTICE QUESTIONS (Integer Type)
Explore 14 Videos
Similar Questions
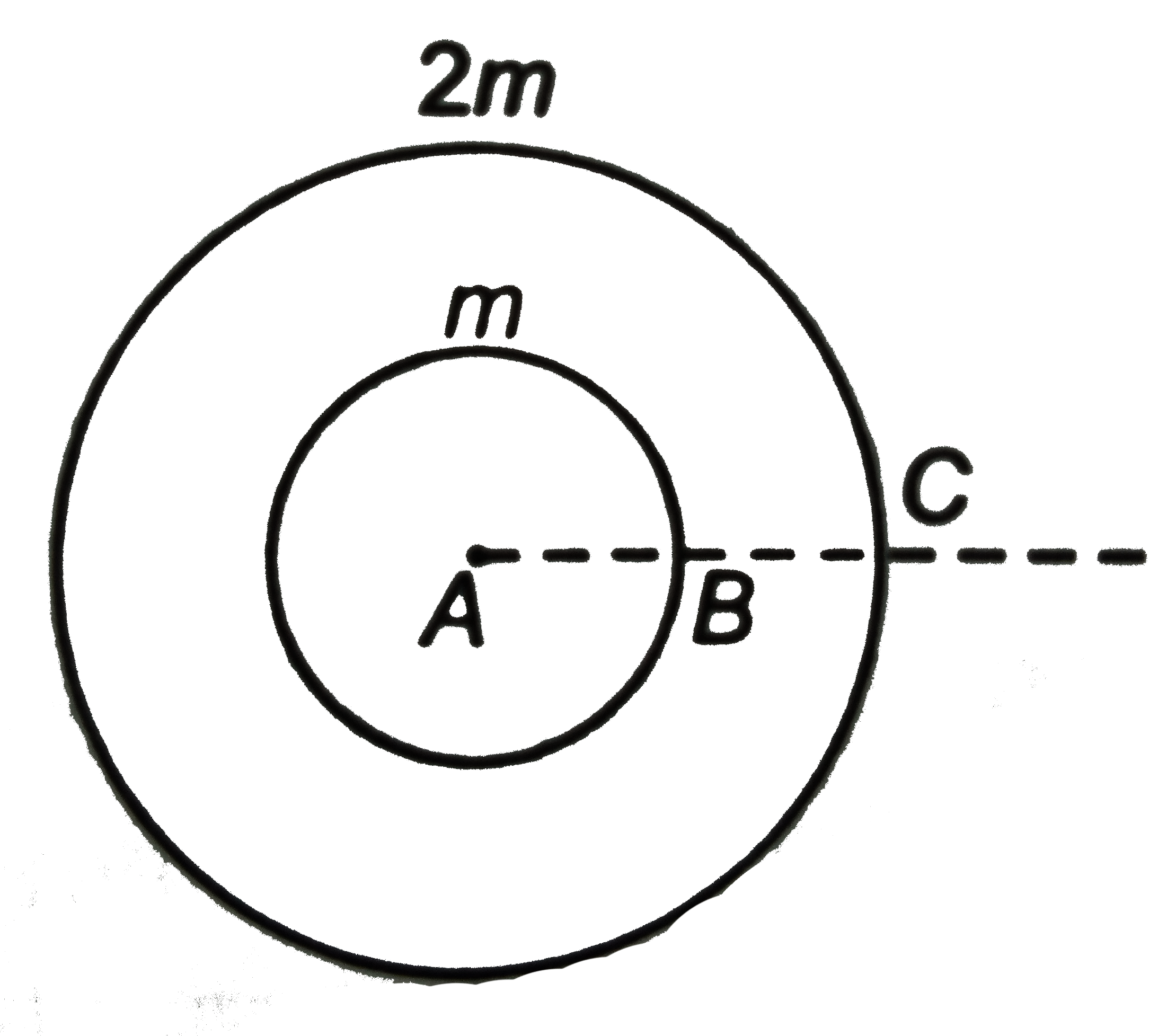
Two spherical shells have masses mand 2m as shows. Choose the correct options.
View SolutionThere are two concentric spherical shells with inner shell having positive charge q and outer shell having a charge -q. Now outer shell is supplied a charge -2g and inner shell is earthed, Calculate the ratio of initial and final capacities of the system. (If a = 3R, b= 5 R)
View Solution
Knowledge Check
Two concentric metallic spherical shells are given positive charges . Then
Athe outer sphere is always at a higher potentialBthe inner sphere is always at a higher potentialCboth the spheres are at the same potentialDno prediction can be made about their potentials unless the actual values of charges and radii are knownTwo concentric metallic spherical shells are given positive charges then
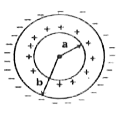
Amore than that of the first conductorBless than that of first conductorCequal to that of first conductorDuncertainTwo concentric spherical shells have charges +q and −q as shown in figure. Choose the correct options.
 AAt a electric field is zero but electric potentiasl in non zeroBAt B electic feid and electric potential both are non zeroCAt C electric field is Zero but electric potential is non zeroDAt C electrilc fiedl and electric potential both are zero
AAt a electric field is zero but electric potentiasl in non zeroBAt B electic feid and electric potential both are non zeroCAt C electric field is Zero but electric potential is non zeroDAt C electrilc fiedl and electric potential both are zero
A metal sphere of radius 'a' is having charge +Q. Now it is connected by a conducting wire concentric spherical shell of radius '2a'. Then the potential at the surface of outer shell is

Here, K=14πε0
View SolutionAssertion: Two concentric charged spherical shells are given. The potential difference between the shells depends on charge of inner shell.
Reason: Potential due to charge of outer shell remains same at every point inside the sphere.
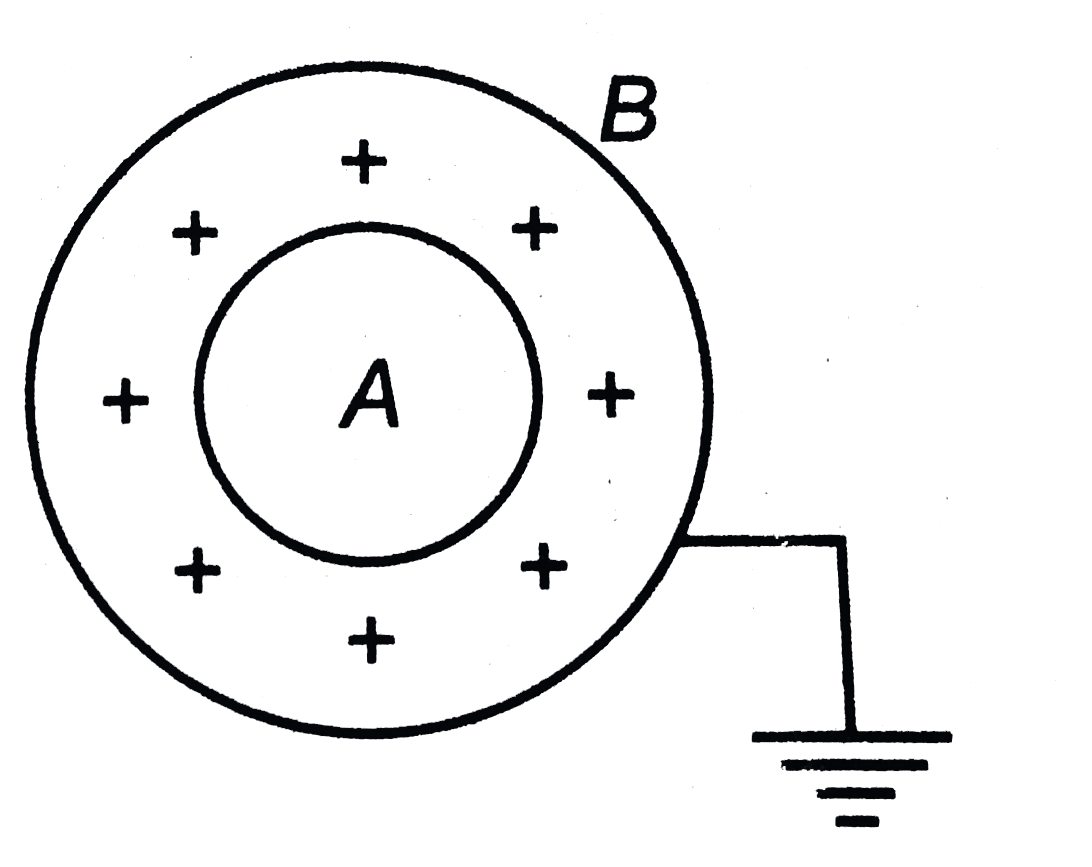
View SolutionA and B are two concentric spherical shells. If A is given a charge +q while B is earthed as shown in figure then
View SolutionWe have an isolated conducting spherical shell of radius 10cm. Some positive charge is given to it so that the resulting electric field has a maximum intensity of 1.8×106NC−1. The same amount of negative charge is given to another isolated conducting spherical shell of radius 20cm. Now, the first shell is placed inside the second so that both are concentric as shown in (Fig. 3.154).
 .
.
If both the spheres are connected by a conducting wire, then.
View SolutionWe have an isolated conducting spherical shell of radius 10cm. Some positive charge is given to it so that the resulting electric field has a maximum intensity of 1.8×106NC−1. The same amount of negative charge is given to another isolated conducting spherical shell of radius 20cm. Now, the first shell is placed inside the second so that both are concentric as shown in (Fig. 3.154).
 .
.
The electric potential at any point inside the first shell is.
View Solution

