Point A is located 0.25 m away from a charge of . Point B is located 0.50 m away from the charge. What is the electric potential difference V_(B)- V_(A) between these two points ?
19 V
26 V
38 V
76 V
The correct Answer is:C
To find the electric potential difference VB−VA between points A and B, we can follow these steps:
Step 1: Understand the formula for electric potential
The electric potential V due to a point charge Q at a distance R is given by the formula:
V=kQR
where k is Coulomb's constant, approximately 9×109N m2/C2.
Step 2: Calculate the electric potential at point A
Point A is located 0.25 m away from the charge −2.1×10−9C. Using the formula:
VA=kQRA=(9×109)×(−2.1×10−9)0.25
Calculating this:
VA=(9×−2.1)0.25=−18.90.25=−75.6V
Step 3: Calculate the electric potential at point B
Point B is located 0.50 m away from the charge. Using the formula:
VB=kQRB=(9×109)×(−2.1×10−9)0.50
Calculating this:
VB=(9×−2.1)0.50=−18.90.50=−37.8V
Step 4: Calculate the electric potential difference
Now, we can find the potential difference VB−VA:
VB−VA=−37.8−(−75.6)=−37.8+75.6=37.8V
Final Answer
The electric potential difference VB−VA is:
37.8V
The electric potential V due to a point charge Q at a distance R is given by the formula:
V=kQR
where k is Coulomb's constant, approximately 9×109N m2/C2.
Point A is located 0.25 m away from the charge −2.1×10−9C. Using the formula:
VA=kQRA=(9×109)×(−2.1×10−9)0.25
Calculating this:
VA=(9×−2.1)0.25=−18.90.25=−75.6V
Point B is located 0.50 m away from the charge. Using the formula:
VB=kQRB=(9×109)×(−2.1×10−9)0.50
Calculating this:
VB=(9×−2.1)0.50=−18.90.50=−37.8V
Now, we can find the potential difference VB−VA:
VB−VA=−37.8−(−75.6)=−37.8+75.6=37.8V
The electric potential difference VB−VA is:
37.8V
Topper's Solved these Questions
- ELECTRIC POTENTIALBook:RESNICK AND HALLIDAYChapter:ELECTRIC POTENTIALExercise:(PRACTICE QUESTIONS) More than One Correct Choice Type
Explore 8 Videos
- ELECTRIC POTENTIALBook:RESNICK AND HALLIDAYChapter:ELECTRIC POTENTIALExercise:(PRACTICE QUESTIONS) Linked Comprehension
Explore 2 Videos
- ELECTRIC POTENTIALBook:RESNICK AND HALLIDAYChapter:ELECTRIC POTENTIALExercise:(PROBLEMS)
Explore 47 Videos
- ELECTRIC CHARGES AND FIELDSBook:RESNICK AND HALLIDAYChapter:ELECTRIC CHARGES AND FIELDSExercise:Practice Questions (Integer Type )
Explore 3 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESNICK AND HALLIDAYChapter:ELECTROMAGNETIC INDUCTIONExercise:PRACTICE QUESTIONS (Integer Type)
Explore 14 Videos
Similar Questions
A solid conducting sphere ofradius 5.0 cm has a charge of 0.25nC distributed uniformly on its surface. If point A is located at the centre of the sphere and a point Bis 15cm from the center, what is the magnitude of the electric potential difference between these two points ?
View SolutionAn infinitely long line of linear charge density λ is shown in the figure. The potential difference VA−VB between the two points A and B is
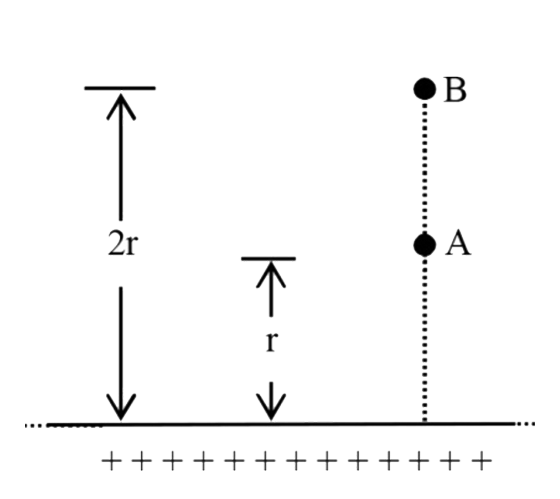
View Solution
Knowledge Check
In figure two points A and B are located in a region of electric field . The potential difference VB−VA is
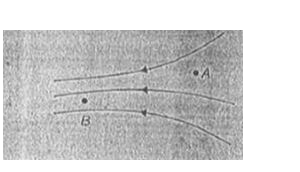 APositiveBNegativeCZeroDNone of these
APositiveBNegativeCZeroDNone of theseThe potential at a point due to charge of 5×10−7C located 10 cm away is
A3.5×105VB3.5×104VC4.5×104VD4.5×105VThe work done in carrying a charge of 5μC form a point A to a point B in an electric field is 10mJ. The potential difference (VB−VA) is then
A+2kVB−2kVC+200VD−200V
A uniform electric field of 30NC−1 exists along the X-axis calculate the potential difference VB−VA between the points A (4m,2m) and B(10m,5m).
View SolutionFind the change in electric potential energy , ΔU as a charge of (a) 2.20×10−6C. (b) −1.10×10−6C moves from a point A to a point given that the change in electric potential between these points is ΔV=VB−VA=24.0V
View SolutionFind the change in electric potential energy, ΔU as a charge of 2.20×10−6C, mass from a point A to point B, given that the change in electric potential between these points is ΔV=VB−VA=24.0V.
View SolutionAsseration: A point charge q is placed at centre of spherical cavity inside a spherical conductor as shown. Another point charge Q is placed outside the conductor as shown. Now as the point charge Q is pushed away from conductor, the potential difference (VA−VB) between two points A and B within the cavity of sphere remains constant.

Reason: The electric field due to charges on outer surface of conductor and outside the conductor is zero at all points inside teh conductor.
View SolutionThe work done in carrying an electron from point A to a point B in an electric is 10 MJ. The potential difference (VB−VA) is then
View Solution

