A particle of charge +7.5μC is released from rest at the point x=60cm on an x axis. The particle begins to move due to the presence of a charge Q that remains fixed at the origin. What is the kinetic energy of the particle at the instant it has moved 50 cm if (a) Q=20μCand(b)Q=−2μC?
To solve the problem, we will use the principle of conservation of energy. The kinetic energy gained by the particle will be equal to the change in electric potential energy as it moves from the initial position to the final position.
Given:
- Charge of the particle, q=+7.5μC=7.5×10−6C
- Initial position, xi=60cm=0.6m
- Final position, xf=50cm=0.5m
(a) When Q=+20μC
1. Calculate Initial Potential Energy Ui:
Ui=kQqri
where ri=0.6m and k=9×109Nm2/C2.
Ui=9×109(20×10−6)(7.5×10−6)0.6
Ui=9×109150×10−120.6=9×109×250×10−12=2.25J
2. Calculate Final Potential Energy Uf:
Uf=kQqrf
where rf=1.1m (since the particle moves from 0.6m to 1.1m).
Uf=9×109(20×10−6)(7.5×10−6)1.1
Uf=9×109150×10−121.1≈1.225J
3. Calculate Change in Potential Energy:
ΔU=Uf−Ui=1.225J−2.25J=−1.025J
4. Calculate Kinetic Energy K:
K=−ΔU=1.025J
(b) When Q=−2μC
1. Calculate Initial Potential Energy Ui:
Ui=kQqri
Ui=9×109(−2×10−6)(7.5×10−6)0.6
Ui=9×109−15×10−120.6=−0.225J
2. Calculate Final Potential Energy Uf:
Uf=kQqrf
where rf=0.1m (since the particle moves from 0.6m to 0.1m).
Uf=9×109(−2×10−6)(7.5×10−6)0.1
Uf=9×109−15×10−120.1=−1.35J
3. Calculate Change in Potential Energy:
ΔU=Uf−Ui=−1.35J−(−0.225J)=−1.125J
4. Calculate Kinetic Energy K:
K=−ΔU=1.125J
Final Answers:
- (a) Kinetic Energy when Q=+20μC: K=1.025J
- (b) Kinetic Energy when Q=−2μC: K=1.125J
- Charge of the particle, q=+7.5μC=7.5×10−6C
- Initial position, xi=60cm=0.6m
- Final position, xf=50cm=0.5m
Ui=kQqri
where ri=0.6m and k=9×109Nm2/C2.
Ui=9×109(20×10−6)(7.5×10−6)0.6
Ui=9×109150×10−120.6=9×109×250×10−12=2.25J
Uf=kQqrf
where rf=1.1m (since the particle moves from 0.6m to 1.1m).
Uf=9×109(20×10−6)(7.5×10−6)1.1
Uf=9×109150×10−121.1≈1.225J
ΔU=Uf−Ui=1.225J−2.25J=−1.025J
K=−ΔU=1.025J
Ui=kQqri
Ui=9×109(−2×10−6)(7.5×10−6)0.6
Ui=9×109−15×10−120.6=−0.225J
Uf=kQqrf
where rf=0.1m (since the particle moves from 0.6m to 0.1m).
Uf=9×109(−2×10−6)(7.5×10−6)0.1
Uf=9×109−15×10−120.1=−1.35J
ΔU=Uf−Ui=−1.35J−(−0.225J)=−1.125J
K=−ΔU=1.125J
- (a) Kinetic Energy when Q=+20μC: K=1.025J
- (b) Kinetic Energy when Q=−2μC: K=1.125J
Topper's Solved these Questions
- ELECTRIC POTENTIALBook:RESNICK AND HALLIDAYChapter:ELECTRIC POTENTIALExercise:(PRACTICE QUESTIONS) Single Correct Choice Type
Explore 21 Videos
- ELECTRIC POTENTIALBook:RESNICK AND HALLIDAYChapter:ELECTRIC POTENTIALExercise:(PRACTICE QUESTIONS) More than One Correct Choice Type
Explore 8 Videos
- ELECTRIC POTENTIALBook:RESNICK AND HALLIDAYChapter:ELECTRIC POTENTIALExercise:CHECKPOINT
Explore 6 Videos
- ELECTRIC CHARGES AND FIELDSBook:RESNICK AND HALLIDAYChapter:ELECTRIC CHARGES AND FIELDSExercise:Practice Questions (Integer Type )
Explore 3 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESNICK AND HALLIDAYChapter:ELECTROMAGNETIC INDUCTIONExercise:PRACTICE QUESTIONS (Integer Type)
Explore 14 Videos
Similar Questions
Identical 50μC charges are fixed on an x axis at x=+±2.0 m. A particle of charge q=15μC is then released from rest at a point on the positive part of they axis. Due to the symmetry of the situation, the particle moves along the y axis and has kinetic energy 1.2 J as it passes through the pointx=0,y=4.0m. (a) What is the kinetic energy of the particle as it passes through the origin? (b) At what negative value of y will the particle momentarily stop?
View SolutionTwo chargess +q and +2q , are held in place on the x axis at the locations x=−d and x=+d respectively. A third charge, +3q , is released from rest on the y axis at y=d. (a) Find the electric potential at the initial location of the third charge. (b) Find the initial electric potential energy of the third charge. (c) What is the kinetic energy of the third charge when it has moved infinity far away from the other two charges ?
View Solution
Knowledge Check
A charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
A2E2t2mqBE2q2r22mCEq2m2t2DEqm2tA charged particle of mass m and charge q is released from rest in an electric field of constant magnitude E. The kinetic energy of the particle after time t is
A2E2t2mqBE2q2t22mCEq2m2t2DEqm2tA particle of mass m and charge q is placed at rest in a uniform electric field E and then released, the kinetic energy attained by the particle after moving a distance y will be
Aq2EyBqEyCaE2yDqEy2
Four point +8μC,−1μC,−1μC, and +8μC are fixed at the points −√27/2m,−√3/2m,+√3/2m, and +√27/2m, respectively, on the y - axis. A particle of mass 6×10−4kg and charge +0.1μC moves along the x- direction. Its speed at x=+∞ is V0. Find the least value of V0 for which the particle will cross the origin. Find also the kinetic energy of the particle at the origin. Find also the kinetic energy of the particle at the origin. Assume that space is gravity free. Given (1/4πε0)=9×109Nm2C−2.
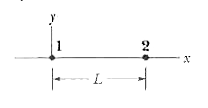
View SolutionIn Fig., particle 1 of charge +6.0μC and particle 2 of charge −2.0μC are held at separation L=10.0cm on an x axis. If particle 3 of unknown charge q3 is to be located such that the net electrostatic force on it from particles 1 and 2 is zero, what must be the (a) x and (b) y coordinates of particle 3 ?
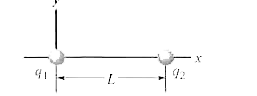
View SolutionTwo charged particles lie along x axis as shown in Fig. The particle with charge q2=+8μC is at x = 6.00 m, and the particle with charge q1=+2μC is at the origin. Locate the point where the resultant electric field is zero.
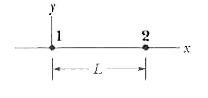
View SolutionIn Fig., particle 1 of charge +q and particle 2 of charge +9.00 q are held at separation L = 8.00 cm on an x axis. If particle 3 of charge q3 is to be located such that the three particles remain in place when released, what must be the (a) x and (b) y coordinates of particle 3, and (c ) the ratio q3/q ?
View SolutionA particle of mass m and charge q is released from rest in uniform electric field of intensity E. Calculate the kinetic energy it attains afect moving a distance x between the plates.
View Solution

