On an interplanetary mission, a 58.5-kg astronaut is floating toward the front of her ship at 0.15 m/s, relative to the ship. She wishes to stop moving, relative to the ship. She decides to throw away the 2.50-kg book she's carrying. What should the speed and direction of the book be to achieve her goal?
0.15 m/s, toward the front of the ship.
3.5 m/s, toward the back of the ship.
3.7 m/s, toward the front of the ship.
0.30 m/s, toward the back of the ship.
The correct Answer is:C
To solve the problem of the astronaut wanting to stop moving relative to the ship after throwing the book, we can use the principle of conservation of momentum. Here’s a step-by-step solution:
Step 1: Understand the initial conditions
The astronaut has a mass of ma=58.5kg and is moving towards the front of the ship at a speed of va=0.15m/s. The mass of the book is mb=2.5kg.
Step 2: Set up the momentum conservation equation
Before the astronaut throws the book, the total momentum of the system (astronaut + book) can be expressed as:
pinitial=(ma+mb)va
Since the book is initially moving with the astronaut, its initial speed is also va=0.15m/s.
Step 3: Determine the final conditions
After throwing the book, the astronaut wants to be at rest relative to the ship, which means her final velocity v′a=0. Let vb be the speed of the book after it is thrown. The direction of vb will be opposite to the direction of the astronaut's initial motion to stop her.
Step 4: Write the final momentum equation
After the book is thrown, the total momentum of the system will be:
pfinal=mav′a+mbvb
Substituting v′a=0:
pfinal=0+mbvb=mbvb
Step 5: Apply conservation of momentum
According to the conservation of momentum:
pinitial=pfinal
Thus,
(ma+mb)va=mbvb
Step 6: Solve for vb
Substituting the values:
(58.5kg+2.5kg)(0.15m/s)=2.5kg⋅vb
Calculating the left side:
61kg⋅0.15m/s=9.15kg m/s
Now, we can solve for vb:
9.15kg m/s=2.5kg⋅vb
vb=9.15kg m/s2.5kg=3.66m/s
Step 7: Determine the direction of vb
Since the astronaut is moving towards the front of the ship and wants to stop, she must throw the book in the opposite direction. Therefore, the speed of the book should be 3.66m/s in the opposite direction.
Final Answer
The speed of the book should be 3.66m/s in the direction opposite to the astronaut's initial motion.
---
The astronaut has a mass of ma=58.5kg and is moving towards the front of the ship at a speed of va=0.15m/s. The mass of the book is mb=2.5kg.
Before the astronaut throws the book, the total momentum of the system (astronaut + book) can be expressed as:
pinitial=(ma+mb)va
Since the book is initially moving with the astronaut, its initial speed is also va=0.15m/s.
After throwing the book, the astronaut wants to be at rest relative to the ship, which means her final velocity v′a=0. Let vb be the speed of the book after it is thrown. The direction of vb will be opposite to the direction of the astronaut's initial motion to stop her.
After the book is thrown, the total momentum of the system will be:
pfinal=mav′a+mbvb
Substituting v′a=0:
pfinal=0+mbvb=mbvb
According to the conservation of momentum:
pinitial=pfinal
Thus,
(ma+mb)va=mbvb
Substituting the values:
(58.5kg+2.5kg)(0.15m/s)=2.5kg⋅vb
Calculating the left side:
61kg⋅0.15m/s=9.15kg m/s
Now, we can solve for vb:
9.15kg m/s=2.5kg⋅vb
vb=9.15kg m/s2.5kg=3.66m/s
Since the astronaut is moving towards the front of the ship and wants to stop, she must throw the book in the opposite direction. Therefore, the speed of the book should be 3.66m/s in the opposite direction.
The speed of the book should be 3.66m/s in the direction opposite to the astronaut's initial motion.
Topper's Solved these Questions
- CENTER OF MASS Book:RESNICK AND HALLIDAYChapter:CENTER OF MASS Exercise:Practice Questions (More than One Correct Choice)
Explore 5 Videos
- CENTER OF MASS Book:RESNICK AND HALLIDAYChapter:CENTER OF MASS Exercise:Practice Questions (Linked Comprehension)
Explore 6 Videos
- CENTER OF MASS Book:RESNICK AND HALLIDAYChapter:CENTER OF MASS Exercise:Problems
Explore 46 Videos
- CAPACITANCEBook:RESNICK AND HALLIDAYChapter:CAPACITANCEExercise:PRACTICE QUESTION (INTEGER TYPE)
Explore 3 Videos
- CIRCUITSBook:RESNICK AND HALLIDAYChapter:CIRCUITSExercise:Practice Questions (Integer Type)
Explore 3 Videos
Similar Questions
A point mass of 1 kg collides elastically with a stationary point mass of 5 kg. After their collision, the 1 kg mass reverses its direction and moves with a speed of 2 m/s. Which of the following statements are correct for the system of these two masses?
View SolutionA 4.0-kg block slides along a frictionless surface with a constant speed of 5.0 m/s as shown. Two seconds after it begins sliding, a horizontal, time-dependent force is applied to the mass. The force is removed 8 s later. The graph shows how the force on the block varies with time.
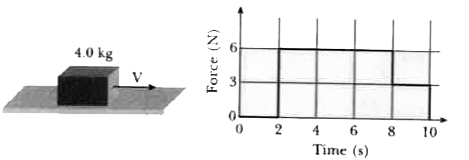
What is the approximate speed of the block at t =11 s?
View SolutionThree particles of masses 1kg, 2kg and 3kg are placed at the corners A, B and C respectively of an equilateral triangle ABC of edge 1m. Find the distance of their centre of mass from A.
View SolutionP and Q are two capacitors with capacitance 10μF and 20μF respectively which are connected in series with a battery of value 12V. Find the ratio between the charges and P and Q.
View SolutionWhen two identical batteries of internal resistance 1Ω each are connected in series across a resistor R, the rate of heat produced in R is J1. When the same batteries are connected in parallel across R, the rate is J_2 = 2.25 J_2thenthevalueofR∈Omega is
View SolutionTwo ships are moving along a line due east. The trailing ship has a speed relative to land based observation point of 64.0(km)/(h) , and the leading ship has a speed of 45.0(km)/(h) relative to that point. The two ships are in a region of the ocean where the current is moving uniformly due west at 10.0(km)/(h) . The trailing ship transmits a sonar signal at a frequency of 1200.0 Hz. What frequency is monitored by the leading ship? Use 1520(m)/(s) as the speed of sound in ocean water.
View SolutionFrom a light-house an observer two ships A and B. Ship A proceeding towards north at a speed 20√2km/h and ship B proceeding towards north-east at a speed of 20km/h. Find in which direction and at what speed the ship B would appear to move to an observer standing on the deck of the ship A.
View SolutionA 50 kg astronaut is floating at rest in space 35 m from her stationary 150,000 kg spaceship. About how long will it take her to float to the ship under the action of the force of gravity?
View SolutionShip A is 10 km due west of ship b . Ship A is heading directly north at a speed of 30 km/h, while ship b is heading in a direction 60^(@) west of north at a speed of 20 km/h . (i) Determine the magnitude of the velocity of ship B relative to ship A . (ii) What will be their distance of closest approach ?
View SolutionAn astronaut is floating in space near her shuttle when she realizes that the cord that's supposed to attach her to the ship has become disconnected. Her total mass (body+suit+equipment) is 91kg. She reaches into her pocket, finds a 1 kg metal tool, and throws it out into space with a velocity of 6m/s directly away from the ship. if the ship is 10 m away, how long will it take her to reach it?
View SolutionA ship is heading west at a speed of 40km per hour. Another ship is heading south at a speed of 30km per hour. Determine the relative velocity of the second ship relative to the first ship.
View SolutionA ship is sailing towards east in a traight line motion, with a speed of 10m//s . A man on the deck is moving across it , towards north, with a speed of 6 m//s calculate the velocity of the man relative to the sea.
View SolutionWhile in Earth's orbit, an 80-kg astronaut carrying a 20-kg tool kit is initially drifting toward a stationary (to her) space shuttle at a speed of 2 m/s. If she throws the tool kit toward the shuttle with a speed of 6 m/s as seen from the shuttle, her final speed is
View SolutionTwo spaceships are observed from Earth to be approaching each other along a straight line. Ship A moves at 0.40c relative to the Earth observer, while ship B moves at 0.50c relative to the same observer. What speed does the captain of ship A report for the speed of ship B?
View SolutionShip A is moving towards south with speed 3m/s and ship B is travelling due west with speed 4m/s Find the velocity of ship B with respect to ship A
View Solution