A student (m = 63 kg) falls freely from rest and strikes the ground. During the collision with the ground, he comes to rest in a time of 0.010 s. The average force exerted on him by the ground is +18,000 N, where the upward direction is taken to be the positive direction. From what height did the student fall ? Assume that the only force acting on him during the collision is that due to the ground.
0.15 m
0.21 m
0.30 m
0.42 m
The correct Answer is:D
To solve the problem step by step, we will follow these steps:
Step 1: Calculate the change in momentum
The average force exerted on the student during the collision with the ground is given as F=18,000N. The time duration of the collision is Δt=0.010s.
Using the impulse-momentum theorem:
FΔt=mΔv
where m is the mass of the student and Δv is the change in velocity. Rearranging gives:
Δv=FΔtm
Step 2: Substitute the known values
Substituting the known values into the equation:
- Mass m=63kg
- Force F=18,000N
- Time Δt=0.010s
Δv=18,000N×0.010s63kg=18063≈2.857m/s
Step 3: Calculate the velocity just before impact
Since the student falls freely from rest, the velocity just before impact v is equal to Δv:
v≈2.857m/s
Step 4: Use the kinematic equation to find the height
Using the kinematic equation for free fall:
v2=2gh
where g is the acceleration due to gravity (approximately 9.8m/s2) and h is the height. Rearranging gives:
h=v22g
Step 5: Substitute the values to find height
Substituting the values:
h=(2.857m/s)22×9.8m/s2=8.16319.6≈0.416m
Step 6: Final answer
Thus, the height from which the student fell is approximately:
h≈0.42m
The average force exerted on the student during the collision with the ground is given as F=18,000N. The time duration of the collision is Δt=0.010s.
FΔt=mΔv
where m is the mass of the student and Δv is the change in velocity. Rearranging gives:
Δv=FΔtm
Substituting the known values into the equation:
- Mass m=63kg
- Force F=18,000N
- Time Δt=0.010s
Since the student falls freely from rest, the velocity just before impact v is equal to Δv:
v≈2.857m/s
Using the kinematic equation for free fall:
v2=2gh
where g is the acceleration due to gravity (approximately 9.8m/s2) and h is the height. Rearranging gives:
h=v22g
Substituting the values:
h=(2.857m/s)22×9.8m/s2=8.16319.6≈0.416m
Thus, the height from which the student fell is approximately:
h≈0.42m
Topper's Solved these Questions
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (More than One Correct Choice)
5 Videos
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Linked Comprehension)
6 Videos
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Problems
46 Videos
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION (INTEGER TYPE)
3 Videos
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)
3 Videos
Similar Questions
A ball of mass m collides with the ground at an angle. With the vertical. If the collision lasts for time t, the average force exerted by the ground on the ball is : (e = coefficient of restitution between the ball and the ground)
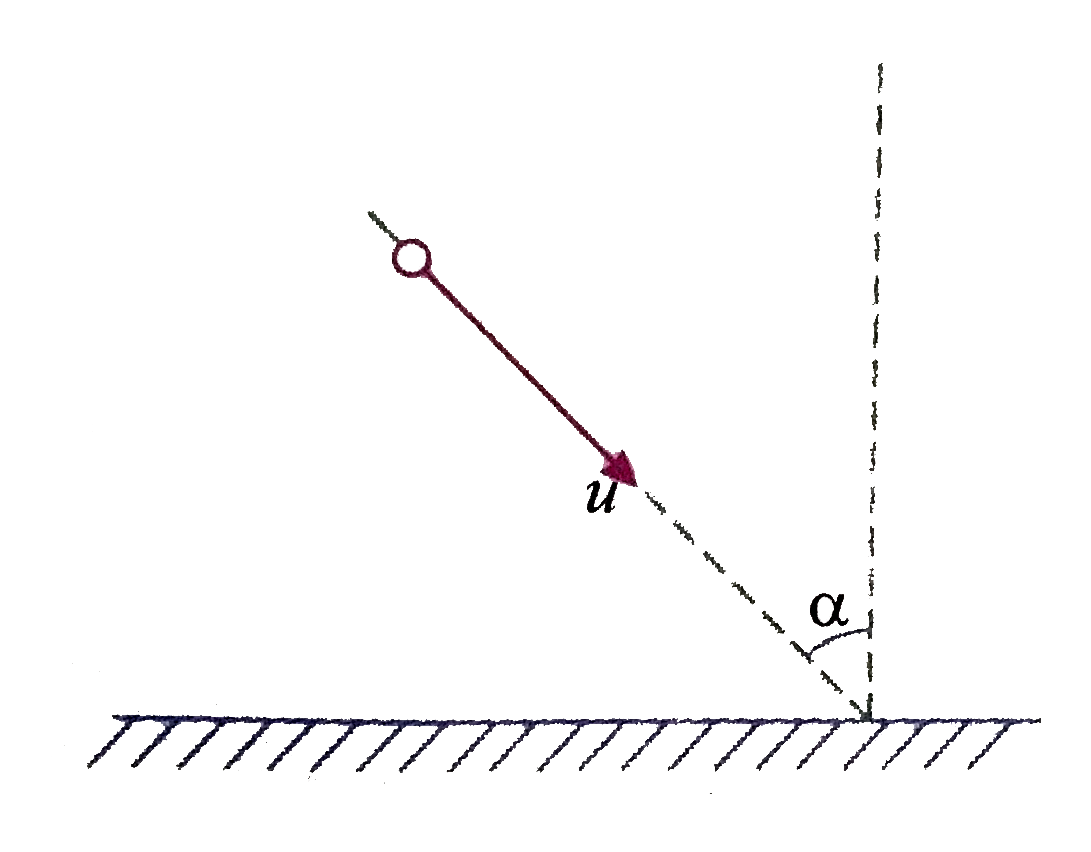 .
.
View SolutionIf the system is left from rest find the time taken by the 8kg block to reach the ground.
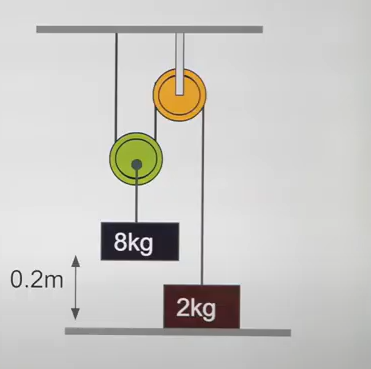
View Solution
Knowledge Check
A parachutist of weight ‘ w ’ strikes the ground with his legs fixed and comes to rest with an upward acceleration of magnitude 3 g . Force exerted on him by ground during landing is
AwB2 wC3 wD4 wA stone falls freely rest. The distance covered by it in the last second is equal to the distance covered by it in the first 2 s. The time taken by the stone to reach the ground is
A2.5sB3.5sC4sD5sAfter falling from a height h and striking the ground twice, a ball rise up to the height [e = coefficient of restitution]
AheBhe2Che3Dhe4
Find the direction of kinetic friction force
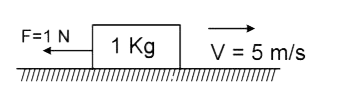
on the block, exerted by the ground.
View SolutionFind the direction of kinetic force
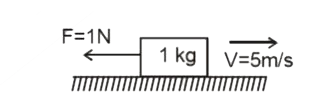
on the block, exerted by the ground.
View SolutionA packet of weight w is dropped with the help of a parachute and on striking the ground comes to rest with retardation equal to twice the acceleration due to gravity. The force exerted on the ground is
View SolutionA stone is allowed to fall freely from rest. The ratio of the time taken to fall through the first metre and the second metre distance is
View SolutionA rock is dropped from rest from a height h above the ground. It falls and hits the ground with a speed of 11 m/s. From what height should the rock be dropped so that its speed on hitting the ground is 22 m/s ? Neglect air resistance.
View Solution
