Two ships are moving along a line due east. The trailing ship has a speed relative to land based observation point of 64.0kmh, and the leading ship has a speed of 45.0kmh relative to that point. The two ships are in a region of the ocean where the current is moving uniformly due west at 10.0kmh. The trailing ship transmits a sonar signal at a frequency of 1200.0 Hz. What frequency is monitored by the leading ship? Use 1520ms as the speed of sound in ocean water.
To solve the problem of determining the frequency monitored by the leading ship, we will follow these steps:
Step 1: Determine the velocities of the ships relative to the medium (water)
1. Trailing Ship Velocity:
- The trailing ship has a speed of 64 km/h relative to land.
- The current is moving at 10 km/h due west (opposite to the direction of the ships).
- Therefore, the velocity of the trailing ship relative to the medium (water) is:
vtrailing=64km/h+10km/h=74km/h
2. Leading Ship Velocity:
- The leading ship has a speed of 45 km/h relative to land.
- Thus, the velocity of the leading ship relative to the medium is:
vleading=45km/h+10km/h=55km/h
Step 2: Convert velocities from km/h to m/s
1. Convert Trailing Ship Velocity:
vtrailing=74km/h×1000m1km×1h3600s≈20.6m/s
2. Convert Leading Ship Velocity:
vleading=55km/h×1000m1km×1h3600s≈15.3m/s
Step 3: Apply the Doppler Effect formula
The Doppler Effect formula for the frequency observed by the leading ship is given by:
f′=f(v+vov−vs)
Where:
- f′ = frequency observed by the leading ship
- f = frequency emitted by the trailing ship = 1200 Hz
- v = speed of sound in water = 1520 m/s
- vo = speed of the observer (leading ship) = 15.3 m/s (moving away from the source)
- vs = speed of the source (trailing ship) = 20.6 m/s (moving towards the observer)
Step 4: Substitute values into the formula
Substituting the values into the formula:
f′=1200Hz(1520+15.31520−20.6)
Calculating the numerator and denominator:
- Numerator: 1520+15.3=1535.3
- Denominator: 1520−20.6=1499.4
Now substituting back:
f′=1200Hz(1535.31499.4)
Step 5: Calculate the final frequency
Calculating the fraction:
1535.31499.4≈1.024
Now, multiplying by the original frequency:
f′≈1200×1.024≈1228.8Hz
Final Answer
The frequency monitored by the leading ship is approximately 1228.8 Hz.
---
1. Trailing Ship Velocity:
- The trailing ship has a speed of 64 km/h relative to land.
- The current is moving at 10 km/h due west (opposite to the direction of the ships).
- Therefore, the velocity of the trailing ship relative to the medium (water) is:
vtrailing=64km/h+10km/h=74km/h
- The leading ship has a speed of 45 km/h relative to land.
- Thus, the velocity of the leading ship relative to the medium is:
vleading=45km/h+10km/h=55km/h
1. Convert Trailing Ship Velocity:
vtrailing=74km/h×1000m1km×1h3600s≈20.6m/s
vleading=55km/h×1000m1km×1h3600s≈15.3m/s
The Doppler Effect formula for the frequency observed by the leading ship is given by:
f′=f(v+vov−vs)
Where:
- f′ = frequency observed by the leading ship
- f = frequency emitted by the trailing ship = 1200 Hz
- v = speed of sound in water = 1520 m/s
- vo = speed of the observer (leading ship) = 15.3 m/s (moving away from the source)
- vs = speed of the source (trailing ship) = 20.6 m/s (moving towards the observer)
Substituting the values into the formula:
f′=1200Hz(1520+15.31520−20.6)
Calculating the numerator and denominator:
- Numerator: 1520+15.3=1535.3
- Denominator: 1520−20.6=1499.4
f′=1200Hz(1535.31499.4)
Calculating the fraction:
1535.31499.4≈1.024
Now, multiplying by the original frequency:
f′≈1200×1.024≈1228.8Hz
The frequency monitored by the leading ship is approximately 1228.8 Hz.
Topper's Solved these Questions
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Examples
56 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Exercise 6.1
56 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger
2 Videos
- SUPERPOSITION AND STANDING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type
5 Videos
Similar Questions
Two train are moving in a straight line in the same direction with a speed of 80 km/h. The relative velocity of one trains w.r.t. each other is
View SolutionTwo ships move from a point at the same time. First ship moves at the speed of 24 km/hr at 45∘ angle from north to east and second ship moves at the speed of 32 km/hr at 75∘ angle from south to east. Find the distance between them after 3 hours.
View SolutionA plane moves in windy weather due east while the pilot the plane somewhat south of east. The wind is blowing at 50 km/h directed 30∘ east of north, while the palne moves at 200 km/h relative to the wind . What is the velocity of the plane relative to the ground and what is the direction in which the pilot points the palne ?
View SolutionA boat moves with speed of 5 km/h relative to water in a river flowing with a speed of 3 km/h and having a width of 1 km. The minimum time taken around a round trip is
View SolutionA particle of mass m moving in the x direction with speed 2v is hit by another particle of mass 2m moving in the y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to
View SolutionTwo ships are sailling in the sea on the two sides of a lighthouse. If the distance between the ships is 10(√3+1) meters and their angle of elevations of the top of the lighthouse are 60∘and45∘, then the height of the lighthouse is (The two ships and the foot of lighthouse are in a straight line)
View SolutionA car A moves along north with velocity 30 km/h and another car B moves along east with velocity 40 km/h. The relative velocity of A with respect to B is
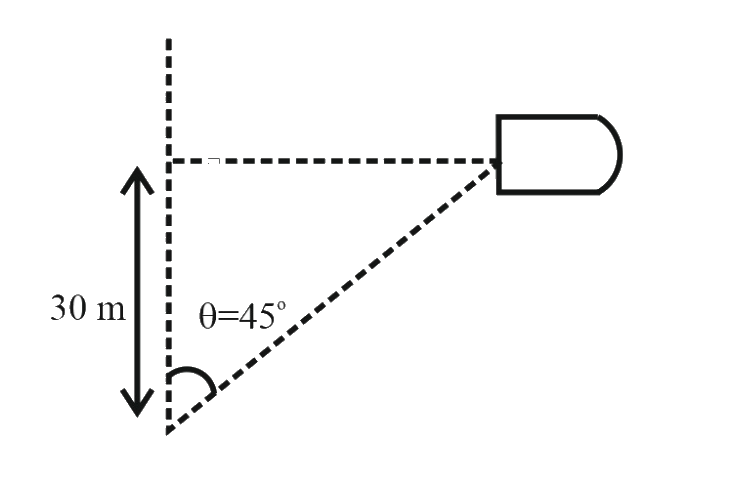
View SolutionA boat is travelling with a speed of 27 km h−1 due east. An observer is situated at 30 m south of the line of travel. The angular velocity of the boat relative to be the observer in the position shown will be
View SolutionA ship 'A' steams down to North at 16 km/h, and ship 'B' due west at 12 km/h. at a certain instant B is 10 km north east of A . find the magnitude of velocity of A relative to B?
View SolutionTwo ships A and B are 10km apart on a line running south to north. Ship A farther north is streaming west at 20km/h and ship B is streaming north at 20km/h. What is their distance of closest approach and how long do they take to reach it?
View Solution
