A 55-kg swimmer is standing on a stationary 210 kg boating raft. The swimmer then runs off the raft horizontally with a velocity of +4.6 m/s relative to the shore. Find the recoil velocity that the raft would have if there were no friction and resistance due to the water.
+1.2 m/s
−1.2 m/s
+0.60 m/s
−2.4 m/s
The correct Answer is:B
To solve the problem, we will use the principle of conservation of momentum. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the system
We have a swimmer with a mass of m=55kg and a raft with a mass of M=210kg. Initially, both the swimmer and the raft are at rest.
Step 2: Write down the initial momentum
Since both the swimmer and the raft are stationary, the initial momentum (pinitial) of the system is:
pinitial=(m+M)⋅0=0
Step 3: Write down the final momentum
When the swimmer runs off the raft with a velocity of vs=+4.6m/s relative to the shore, the raft will have a recoil velocity vr in the opposite direction. The final momentum (pfinal) of the system can be expressed as:
pfinal=m⋅vs+M⋅vr
Substituting the values, we have:
pfinal=55⋅4.6+210⋅vr
Step 4: Apply conservation of momentum
According to the conservation of momentum:
pinitial=pfinal
Thus, we have:
0=55⋅4.6+210⋅vr
Step 5: Solve for the raft's velocity
Now, we can solve for vr:
210⋅vr=−55⋅4.6
vr=−55⋅4.6210
Calculating the right side:
vr=−253210≈−1.2m/s
Conclusion
The recoil velocity of the raft is approximately −1.2m/s. The negative sign indicates that the raft moves in the opposite direction to the swimmer.
We have a swimmer with a mass of m=55kg and a raft with a mass of M=210kg. Initially, both the swimmer and the raft are at rest.
Since both the swimmer and the raft are stationary, the initial momentum (pinitial) of the system is:
pinitial=(m+M)⋅0=0
When the swimmer runs off the raft with a velocity of vs=+4.6m/s relative to the shore, the raft will have a recoil velocity vr in the opposite direction. The final momentum (pfinal) of the system can be expressed as:
pfinal=m⋅vs+M⋅vr
Substituting the values, we have:
pfinal=55⋅4.6+210⋅vr
According to the conservation of momentum:
pinitial=pfinal
Thus, we have:
0=55⋅4.6+210⋅vr
Now, we can solve for vr:
210⋅vr=−55⋅4.6
vr=−55⋅4.6210
Calculating the right side:
vr=−253210≈−1.2m/s
The recoil velocity of the raft is approximately −1.2m/s. The negative sign indicates that the raft moves in the opposite direction to the swimmer.
Topper's Solved these Questions
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (More than One Correct Choice)
5 Videos
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Practice Questions (Linked Comprehension)
6 Videos
- CENTER OF MASS BOOK - RESNICK AND HALLIDAYCHAPTER - CENTER OF MASS EXERCISE - Problems
46 Videos
- CAPACITANCEBOOK - RESNICK AND HALLIDAYCHAPTER - CAPACITANCEEXERCISE - PRACTICE QUESTION (INTEGER TYPE)
3 Videos
- CIRCUITSBOOK - RESNICK AND HALLIDAYCHAPTER - CIRCUITSEXERCISE - Practice Questions (Integer Type)
3 Videos
Similar Questions
A man of mass m1 = 80 kg is standing on a platform of mass m2 = 20 kg that lies on a frictionless horizontal surface. The man starts moving on the platform with a velocity vr = 10 m/s relative to the platform. Find the recoil speed of the platform.
View SolutionA person P of mass 50 kg stands at the middle of a boat of mass 100 kg moving at a constant velocity 10 m/s with no friction between water and boat and also the engine of the boat is shut off. With what velocity (relative to the boat surface) should the person move so that the boat comes to rest. Neglect friction between water and boat.
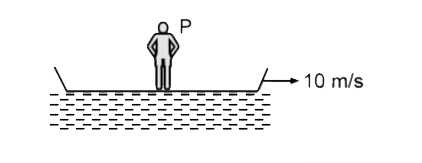
View Solution
Knowledge Check
A dog weighing 5kg is standing on a flat boat so that it is 10 metres from the shore. It walks 4m on the boat towards the shore and then halts. The boat weighs 20kg and one can assume that there is no friction between it and water. The dog from the shore at the end of this time is
A3.4mB6.8mC12.6mD10mA wagon of 200kg is moving on a smooth track with velocity of 2m/sec. A man of 80kg also runs in the wagon with a velocity such that speed of the centre of mass of the system is zero. Find the velocity of man relative to the wagon (in m//s).
A5B6C7D8A small ball of mass 1kg strikes a wedge of mass 4kg horizontally with a velocity of 10m/s. Friction is absent everywhere and collision is elastic. Select the incorrect answer:
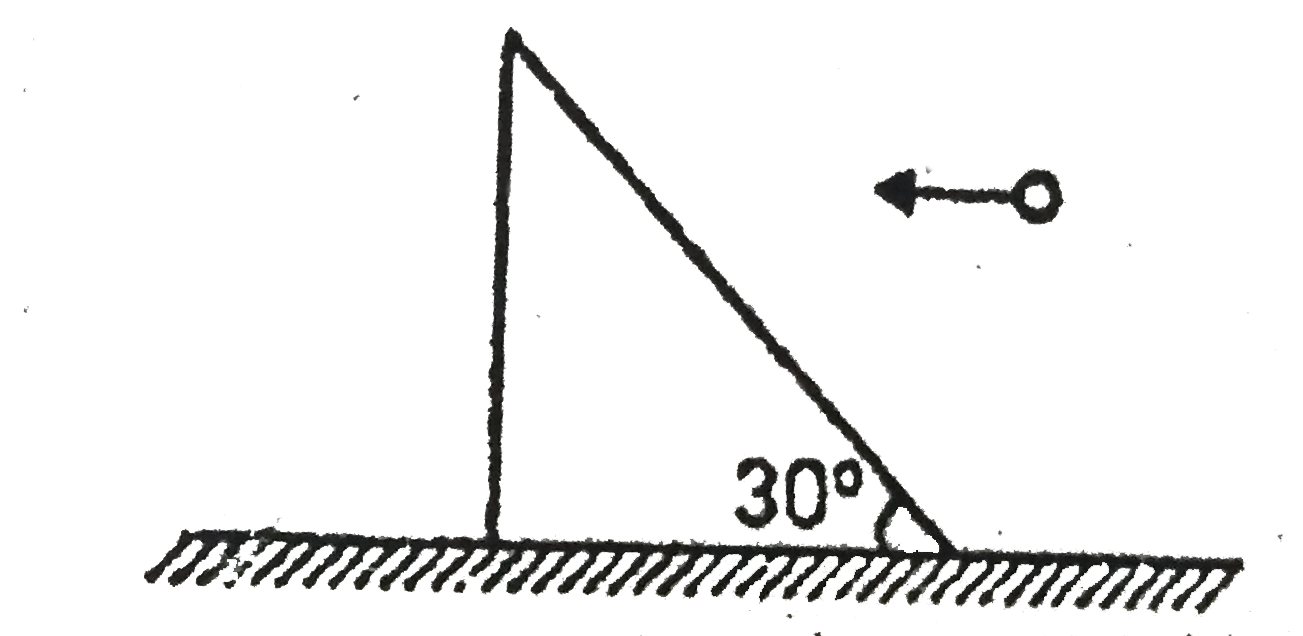 Athe horizontal component of linear momentum of the system (wedge+ball ) during the collision will remain conservedBthe linear momentum of the system (wedge+ball) will remain conserved during the collisionCthe component of linear momentum of the ball along common tangent will remain same during the collisionDthe linear momentum of the ball along common normal will change during collision
Athe horizontal component of linear momentum of the system (wedge+ball ) during the collision will remain conservedBthe linear momentum of the system (wedge+ball) will remain conserved during the collisionCthe component of linear momentum of the ball along common tangent will remain same during the collisionDthe linear momentum of the ball along common normal will change during collision
A buggy of mass 100 kg is free to move on a frictionless horizontal track. Two men, each of mass 50 kg, are standing on the buggy, which is initially stationary. The men jump off the buggy with velocity =10m/s relative to the buggy. In one situation, the men jump one after the other. in another situation, the men jump simultaneously. what is the ratio of the velocities of the buggy in two cases?
View SolutionA ball of mass 4kg moving with a velocity of 12m/s impinges directly on another ball of mass 8kg moving with velocity of 4m/s in the same direction. Find their velocities after impact and calculate the loss of KE due to impact if e=0.5.
View SolutionA person stands in a stationary canoe and throws a 5.00-kg stone with a velocity of 8.00 m/s at an angle of 30.0∘ above the horizontal. The person and canoe have a combined mass of 105 kg. Ignoring air resistance and effects of the water, find the horizontal recoil velocity (magnitude and direction of the canoe. Assume the hori zontal component of the velocity of the stone is in the +x direction.
View SolutionA man weighing 60 kg is standing on a trolley weighting 240 kg. The trolley is resting on frictionless horizontal rails. If the man starts walking on the trolley with a velocity of 1 m/s, then after 5s, his displacement relative to the ground is
View SolutionA flat uniform circular disk (radius = 2.00 m, mass=1.00×102 kg) is initially stationary. The disk is free to rotate in the horizontal plane about a frictionless axis perpendic ular to the center of the disk. A 40.0-kg person, standing 1.25 m from the axis, begins to run on the disk in a circular path and has a tangential speed of 2.00m/s relative to the ground. Find the resulting angular speed of the disk (in rad/s) and describe the direction of the rotation.
View Solution
