A copper rod of cross sectional area A carries a uniform current I through it. At temperature T if the volume charge density of the rod is ρ how long will the charges take to travel a distance d?
2ρdAIT
2ρdAI
ρdAI
ρdAIT
The correct Answer is:C
Charge density ρ=chargevolume=qAd⇒q=ρAd
Also, q=IT⇒T=(q)(I)=ρADI
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DISHA PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-1 Concept Builder (Topicwise) Topic 1: Electric Current, Drift of Electrons and Ohm.s Low
13 Videos
- CURRENT ELECTRICITYBOOK - DISHA PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-1 Concept Builder (Topicwise) Topic 2: Resistance, Conductance and Resistivity
14 Videos
- CONCEPT BUILDERBOOK - DISHA PUBLICATIONCHAPTER - CONCEPT BUILDEREXERCISE - Exercise-2 Concept Applicator
27 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - DISHA PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - EXERCISE -2 : CONCEPT ALLPLICATOR
30 Videos
Similar Questions
Find the velocity of charge leading to 1A current which flows in a copper conductor of cross section 1cm2 and length 10km. Free electron density of copper is 8.5x1028/m3. How long will it take the electric charge to travel from one end of the conductor to the other?
View SolutionAB is a uniformly shaped rod of length L and cross sectional are S, but its density varies with distance from one end A of the rod as ρ=px2+c, where p and c are positive constants. Find out the distance of the centre of mass of this rod from the end A.
View Solution
Knowledge Check
A metal rod of length 'L' and cross-sectional area 'A' is heated through 'T'∘C What is the force required to prevent the expansion of the rod lengthwise ?
AYAαT(1−αT)BYAαT(1+αT)C(1−αT)YAαTD(1+αT)YAαTA straight conductor of uniform cross section carries a time varying current, which varies at the rate dI//dt = I. If s is the specific charge that is carried by each charge carries of the conductor and l is the length of the condcutor, then the totalt force experienced by all the charge carries per unit length of the conductor due to their drift velocities only is
AF=IsBF=I2√lsCF=IsDF=2IlsTwo rods of copper and iron with the same cross sectional area are joined at S and a steady current i flows through the rods as shown in the figure

Choose the most appropriate representation of charges accumulated near the junction S.A B
B C
C D
D
A long cylinder of uniform cross section and radius R is carrying a current i along its length and current density is uniform cross section and radius r in the cylinder parallel to its length. The axis of the cylinderical cavity is separated by a distance d from the axis of the cylinder. Find the magnetic field at the axis of cylinder.
View SolutionThe KE and moment of inertia about the given end point of a rod of mass m and length l and cross sectional area A which is rotating with ω=√gl as shown in figure. Will be [density of the rod varies as ρ=ρ0(1+xl),x is the distance measured from O)n ]
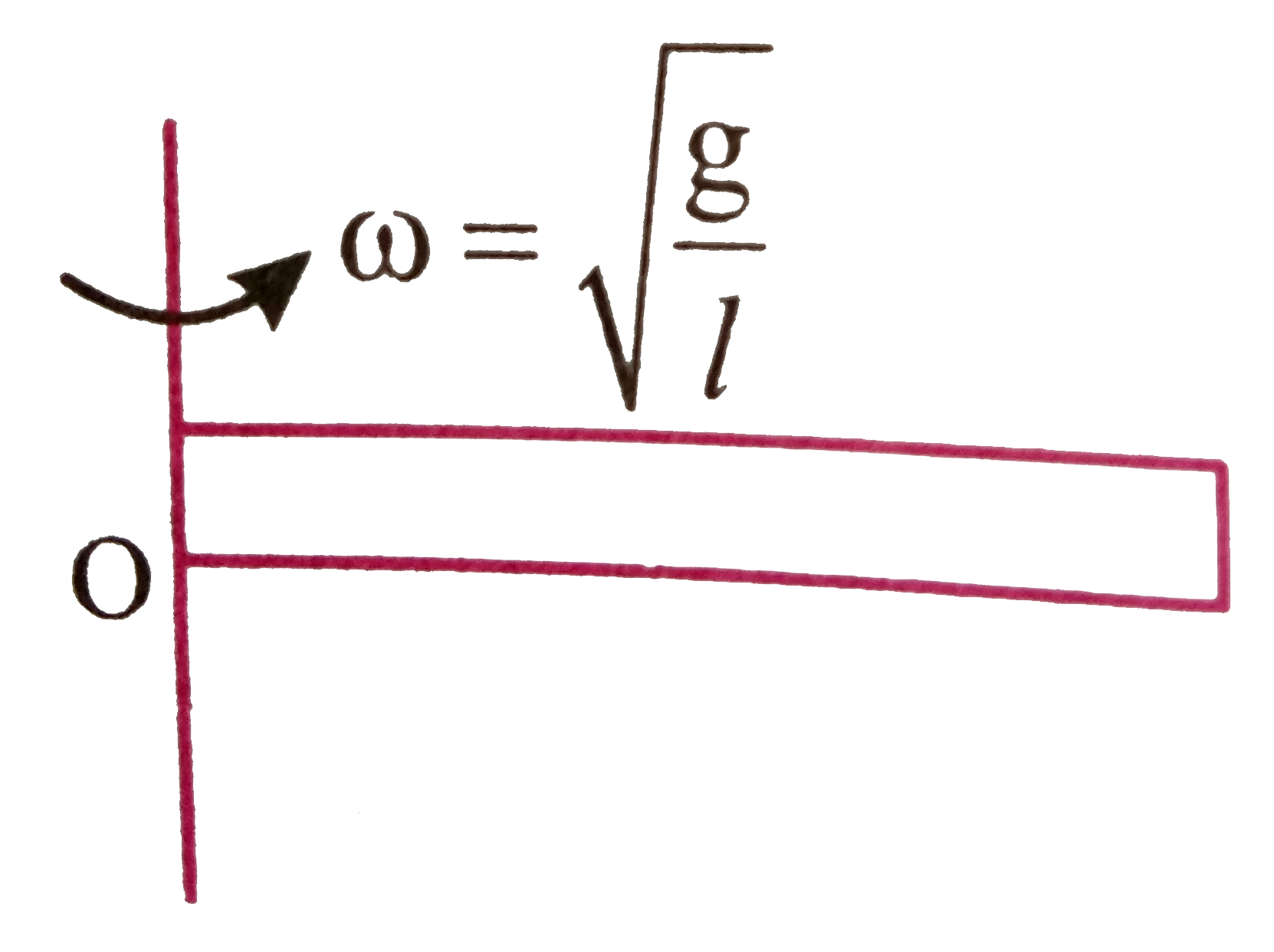
View SolutionA conducting cylindrical rod of uniform cross-sectional area is kept between two large chambers which are at temperatures 100∘C and 0∘C, respectively. The cconductivety of the rod increases with x, where x is distance from 100∘C end. The temperature profile of the rod in steady -state will be as

View SolutionA conductor of area of cross-section. A having charge carries, each having a charge q is subjected to a polential difference V. The number density of charge carries in the conductor is an und the charge carries (along with Their random) are moving with a velocity. If s is the conductivity of the conductor and ris the average relaxation
View SolutionA very long, strainght, thin wire carries −3.60nCm−1 of fixed negative charge. The wire is to be surrounded by a uniform cylinder of positive charge, radius 1.50 cm, coaxial with the wire. The volume charge density ρ of the cylinder is to be selected is zero. Calculate the required positive charge density ρ (in μCm−3).
View Solution
