A cell when balanced with potentiometer gave a balance length of50 cm. 4.5Ω external resistance is introduced in the circuit, now it is balanced on 45 cm. The internal resistance of cell is
0.25Ω
0.5Ω
1.0Ω
1.5Ω
The correct Answer is:A
To find the internal resistance of the cell, we can follow these steps:
Step 1: Understand the Initial Conditions
Initially, the balance length with the potentiometer was 50 cm. This means that the electromotive force (EMF) of the cell (E) can be expressed as:
E=λ×50
where λ is the potential gradient (voltage per unit length) of the potentiometer wire.
Step 2: Introduce External Resistance
When a 4.5 ohm external resistance is introduced, the new balance length is 45 cm. The potential drop across the external resistance can be expressed as:
Vext=λ×45
Step 3: Relate Current to Potential Drop
Let I be the current flowing through the circuit. The potential drop across the external resistance is also given by Ohm's Law:
Vext=I×4.5
Thus, we can equate the two expressions for the potential drop:
λ×45=I×4.5
Step 4: Solve for Current
From the equation above, we can express the current I:
I=λ×454.5
This simplifies to:
I=10λ
Step 5: Apply Kirchhoff's Loop Law
According to Kirchhoff's Loop Law, the EMF of the cell is equal to the sum of the potential drops across the internal resistance and the external resistance:
E=I×r+I×4.5
Substituting E and I into this equation gives:
50λ=(10λ)×r+(10λ)×4.5
Step 6: Simplify the Equation
We can factor out 10λ:
50λ=10λ(r+4.5)
Dividing both sides by 10λ (assuming λ≠0):
5=r+4.5
Step 7: Solve for Internal Resistance
Now, we can solve for the internal resistance r:
r=5−4.5
r=0.5Ω
Conclusion
The internal resistance of the cell is 0.5Ω.
---
Initially, the balance length with the potentiometer was 50 cm. This means that the electromotive force (EMF) of the cell (E) can be expressed as:
E=λ×50
where λ is the potential gradient (voltage per unit length) of the potentiometer wire.
When a 4.5 ohm external resistance is introduced, the new balance length is 45 cm. The potential drop across the external resistance can be expressed as:
Vext=λ×45
Let I be the current flowing through the circuit. The potential drop across the external resistance is also given by Ohm's Law:
Vext=I×4.5
Thus, we can equate the two expressions for the potential drop:
λ×45=I×4.5
From the equation above, we can express the current I:
I=λ×454.5
This simplifies to:
I=10λ
According to Kirchhoff's Loop Law, the EMF of the cell is equal to the sum of the potential drops across the internal resistance and the external resistance:
E=I×r+I×4.5
Substituting E and I into this equation gives:
50λ=(10λ)×r+(10λ)×4.5
We can factor out 10λ:
50λ=10λ(r+4.5)
Dividing both sides by 10λ (assuming λ≠0):
5=r+4.5
Now, we can solve for the internal resistance r:
r=5−4.5
r=0.5Ω
The internal resistance of the cell is 0.5Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DISHA PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - EXERCISE-1 Concept Builder (Topicwise) Topic 5: Electrical Energy, Power and Heating Effect of Current
17 Videos
- CONCEPT BUILDERBOOK - DISHA PUBLICATIONCHAPTER - CONCEPT BUILDEREXERCISE - Exercise-2 Concept Applicator
27 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - DISHA PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - EXERCISE -2 : CONCEPT ALLPLICATOR
30 Videos
Similar Questions
In potentiometer experiment, a cell is balanced by length 120 cm. When a cell is shunted by resistance of 5Ω, the balancing length is 80 cm. The internal resistance of cell is
View SolutionA cell is balanced on 125 cm length of a potentiometer wire. Now the cell is short circuited by a resistance of 2 Ω and the balance is obtained at 100 cm. The internal resistance of the cell is ____.
View Solution
Knowledge Check
In an experiment to determine the internal resistance of a cell with potentiometer, the balancing length is 165 cm. When a resistance of 5 ohm is joined in parallel with the cell the balancing length is 150 cm. The internal resistance of cell is
A2.2ΩB1.1ΩC3.3ΩD0.5ΩIn potentiometer experiment, a cell is balanced by length 120cm. When a cell is shunted by resistance of 5Ω, the balancing length is 80 cm. The internal resistance of cell is
A2.5ΩB3ΩC4ΩD5ΩThe emf of cell is balanced by balancing length 450 cm . When the resistance of 10Ω is connected across the cell, balancing length changes by 100 cm. The internal resistance of a cell is
A1.8ΩB2.8ΩC3.8ΩD2.5Ω
In a potentiometer experiment the balancing length with a cell is 560 cm. When an external resistance of 10Ω is connected in parallel to the cell, the balancing length changes by 60 cm. Find the internal resistance of the cell.
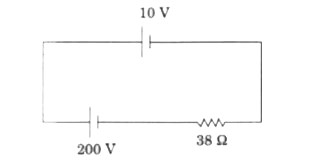
View SolutionA 10 V cells of negligible internal resistance is connected in parallel across a battery of emf 200 V and internal resistance 38Q . As shown in the figures , Find the value of current in the circuit
In a potentiometer arrangement for determining the emf . of a cell the balance point of the cell in open circuit is 350 cm. When a resistance of 9Q . is used in the external circuit of the cells the balance point shift to 300 cm. Determine the internal resistance of the cell.
View SolutionIn a potentiometer experiment, the balancing length with a cell is 560cm. When an external resistance of 10ohms is connected in parallel to the cell the balancing length changs by 60cm. The internal resistance of the cell in ohm is
View SolutionThe e.m.f. of a standard cell balances across 150 cm length of a wire of potentiometer. When a resistance of 2Ω is connected as a shunt with the cell, the balance point is obtained at 100cm . The internal resistance of the cell is
View SolutionA 2.0 V potentiometer is used to determine the internal resistance of 1.5V cell. The balance point of the cell in the circuit is 75cm. When a resistor of 10Ω is connected across cel, the balance point sifts to 60cm. The internal resistance of the cell is
View Solution
