Figure showns a planet in an elliptical orbit around the sun S. Where is the kinetic energy of the planet maximum?

A
A
B
B
C
C
D
D
Video Solution
Text Solution
The correct Answer is:A
Angular momentum is conserved. At A, the moment of inertia is least and hence angular speed is maximum. Thus the K.E.at A is maximum.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - DISHA PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - EXERCISE-230videos
GRAVITATION
- BOOK - DISHA PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - EXERCISE-230videos
GRAVITATION
- BOOK - DISHA PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE 2: CONCEPT APPLICATOR24videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - DISHA PUBLICATIONCHAPTER - JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))EXERCISE - QUESTIONS30videos
JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))
Similar Questions
Knowledge Check
- Question 1 - Select One
Figure shows a planet in an elliptical orbit around the Sun S. Where is the kinetic energy of the planet maximum?
 AP1BP2CP3DP4
AP1BP2CP3DP4 - Question 2 - Select One or More
In elliptical orbit of a planet
Aangular momentum about centre of sun is constantBpotential energy is constantCkinetic energy is constantDtotal mechanical energy is constant - Question 3 - Select One
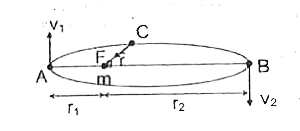
A planet revolves in elliptical orbit around the sun. (see figure). The linear speed of the planet will be maximum at
 AABBCCDD
AABBCCDD
A planet revolves around the sun in an elliptical . The linear speed of the planet will be maximum at
 View Solution
View SolutionFor motiion of planets in ellipticla orbits around the sun the central force is
View SolutionConsider a planet moving in an elliptical orbit around the Sun. The work done on the planet by the gravitational force of the Sun
View SolutionA planet is orbiting the sun is an elliptical orbit. Let U denote the potential energy and K denote the kinetic energy of the planet at an arbitrary point on the orbit. Choose the correct statement -
View SolutionAsteroids revolve around the sun between the orbits of the planets :
View Solution