Two masses m1 and m2(m1<m2) are released from rest from a finite distance. They start under their mutual gravitational attraction
acceleration of m1 is more than that of m2
acceleration of m2 is more than that of m1
centre of mass of system will remain at rest in all the reference frame
total energy of system does not remains constant
The correct Answer is:B
Same force acts on both masses
Hence a ∝1m (F = ma)
In absence of external force (remember mutual) gravitational force is an internal force for the system ) total energy remains constant .
Topper's Solved these Questions
- GRAVITATIONBOOK - DISHA PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - EXERCISE-2
30 Videos
- GRAVITATIONBOOK - DISHA PUBLICATIONCHAPTER - GRAVITATIONEXERCISE - EXERCISE-2
30 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - DISHA PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - EXERCISE 2: CONCEPT APPLICATOR
24 Videos
- JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))BOOK - DISHA PUBLICATIONCHAPTER - JEE MAINS- 2019 (HELD ON :9TH APRIL 2019 (SHIFT-I))EXERCISE - QUESTIONS
30 Videos
Similar Questions
In a double star, two stars one of mass m1 and another of mass m2, with a separation d, rotate about their common centre of mass. Find
(a) an expression for their time period of revolution.
(b) the ratio of their kinetic energies.
(c) the ratio of their angular momenta about the centre of mass.
(d) the total angular momentum of the system.
(e) the kinetic energy of the system.
View SolutionTwo bodies of masses m1 and m2 are initially at infinite distance at rest. Let they start moving towards each other due to gravitational attraction. Calculate the (i) ratio of accelerations and (ii) speeds at the point where separation between them becomes r.
View Solution
Knowledge Check
Two masses m1 and m2(m1<m2) are released from rest finite distance. They start under their mutual gravitational attraction-
Aacceleration of m1 is more than that of m2Bacceleration of m2 is more than that of m1Ccentre of mass of system will remain at rest in all the references frame.Dtotal energy of system remains constantTwo particles of masses m1andm2 are intially at rest at an infinite distance apart. If they approach each other under their mutual interaction given by F=−Kr2. Their speed of approach at the instant when they are at a distance d apart is
A√2Kd[1m1+1m2]B√2Kd[1m1−1m2]C√2Kd[m1m2m1+m2]D√2Kd[m1m2m1−m2]A smooth massless string passes over a smooth fixed pulley. Two masses m1 and m2(m1>m2) are tied at the two ends of the string. The masses are allowed to move under gravity starting from rest. The total external force acting on the two masses is
A(m1+m2)gB(m1−m2)2m1+m2gC(m1−m2)gD(m1+m2)2m1−m2g
Two particles of masses m1 and m2 initially at rest a infinite distance from each other, move under the action of mutual gravitational pull. Show that at any instant therir relative velocity of approach is √2G(m1+m2)/R where R is their separation at that instant.
View SolutionTwo particles m1 and m2 are initially at rest at infinite distance. Find their relative velocity of approach due to gravitational attraction when their separation is d.
View SolutionConsider a system of two particles of masses m1 and m2 separated by a distance r. Suppose they start to move towards each other due to their mutual attraction (attractive force may be electrical, gravitational, etc.).
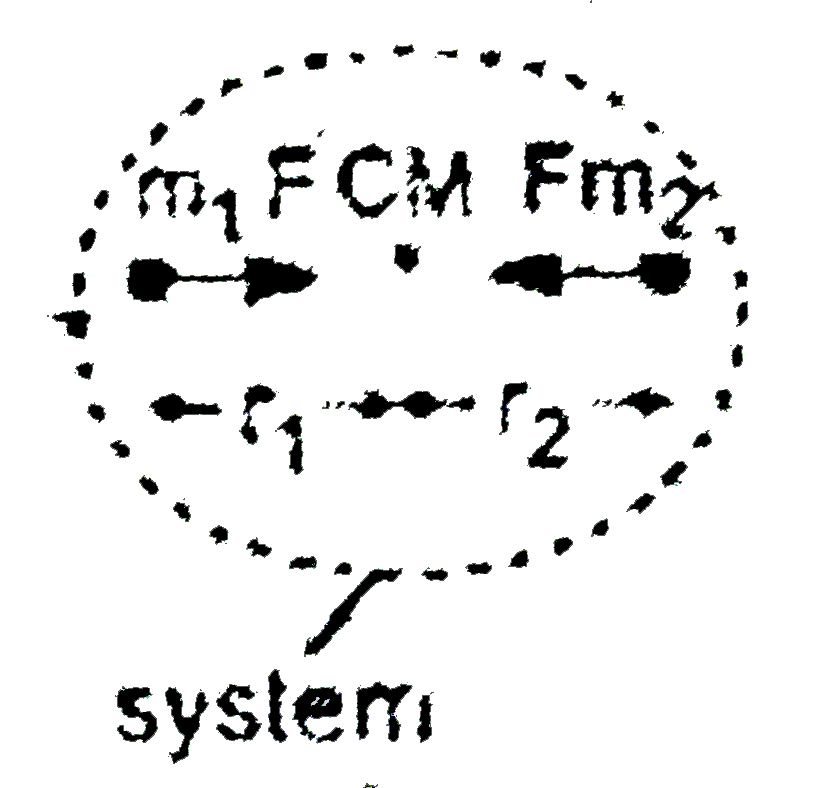
View SolutionTwo bodies of mass m1andm2 are initially at rest placed infinite distance apart. They are then allowed to move towards each other under mutual gravitational attaction. Show that their relative velocity of approach at separation r betweeen them is
v=√2G(m1+m2)r
View SolutionTwo objects of masses m and 4m are at rest at an infinite separation. They move towards each other under mutual gravitational attraction. If G is the universal gravitaitonal constant, then at separation r
View Solution
